Practical application of triangle similarity. Publication by a teacher on the topic Practical applications of similarity of triangles

"Chernovskaya secondary school", branch of "Sychevskaya secondary school named after K.F. Lebedinskaya"

Math lesson in 8th grade on the topic “Practical applications of similarity of triangles”

Prepared by: Nikitina Galina Vasilievna - mathematics teacher

Lesson motto:

“Theory without practice is dead or fruitless; practice without theory is impossible or harmful. Theory requires knowledge, and practice requires skills.”

“Sooner or later, every correct mathematical idea finds application in one thing or another.”

Alexey Nikolaevich Krylov

From the history…

Determining the height of a pyramid

From the history…

Determining the height of a pyramid

Measuring the height of an object

• By the shadow

Using a pole.

Using a mirror

A ray of light FD, reflected from a mirror at point D, enters the human eye (point B)

Mirror

 ABD  DFE (two corners):

 VAD =  FED=90°;

 1 =  2

Mirror

A 1

Δ A 1 B 1 C~Δ ABC

A

WITH 1

IN

WITH

The world around us is a world of geometry, pure, true, impeccable in our eyes. Everything around is geometry. Le Corbusier

Geometry is a science that has all the properties of crystal glass, equally transparent in reasoning, impeccable in evidence, clear in answers, harmoniously combining the transparency of thought and the beauty of the human mind. Geometry is not a fully understood science, and perhaps many discoveries await you. I wish you good luck in your further study of science.

"Ladder of Achievement"

Today in class I learned...

It was interesting to me..

It was difficult for me...

I realized that...

I felt that...

Most of all I liked…

I am satisfied with my work in class (not really, not satisfied) because...

Geometry lesson in 8th grade on the topic "Practical application of the similarity of triangles" for the 2016-2017 academic year.

""Geometry is the most powerful
a means to sharpen our mental
abilities and gives the opportunity to correctly
think and reason."
G. Galileo

The purpose of the lesson: teach to apply theoretical knowledge to solve problems with practical content.

Tasks:

Educational:

summarize and systematize knowledge on the topic: “Signs of similarity of triangles”;

development of skills to generalize, abstract and concretize the properties of the objects and relationships being studied, and apply them in solving practical problems;

continue to develop students’ skills in using signs of similarity of triangles when solving problems.

Educational:

develop logical thinking, ability to compare, generalize, draw conclusions;

develop students' interest in the subject being studied;

development creativity students

development of skills to generalize, abstract and concretize the properties of the objects and relationships being studied, and apply them in solving practical problems

Educational:

to form motives for cognitive activity,

aesthetic education of students.

developing the ability to assess your level of knowledge of a topic;

development of a culture of oral speech, cognitive interest;

Equipment :

• multimedia projector, screen;

  presentation to accompany the lesson ;

  Handout.

Lesson type: practical seminar on problem solving

Lesson structure:

Organizing time.

Update background knowledge:
A) checking students' knowledge of learning;
b) repetition theoretical material;
V) oral problem solving.

Psychological relief

Problem Solving Workshop: Solving fun problems.

A minute of exercise (for the eyes, to relieve tension from the shoulder girdle)

Additional material

Homework.

Group work

Lesson summary. Reflection. Self-esteem

Used Books:

Geometry, 7-9: textbook. for general education institutions/ [L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al.] – 16th ed. – M.: Enlightenment; JSC "Moscow" textbook", 2006

Studying geometry in grades 7-9: Method. recommendations for studies: Book. for the teacher/ L.S. Atanasyan, V.F. Butuzov, Yu.A. Glazkov and others - M.: Education, 1997.

AND I. Depman World of numbers. Stories about mathematics. – L.: Children's literature, 1975.

During the classes

I. Organizational moment.

II. A word from the teacher about the purpose of this lesson.

A triangle is the simplest geometric figure familiar to us since childhood. We turn to the triangle most often in geometry lessons. This figure is fraught with a lot of interesting and mysterious things, like Bermuda Triangle, in which ships and planes disappear without a trace.One sage said: “The highest manifestation of the spirit is the mind. The highest manifestation of the mind is geometry. The geometry cell is a triangle. He is as inexhaustible as the Universe.” This is one of the main topics of the school planimetry course. The ability to solve problems using similarity features is widely used in geometry, physics, and astronomy.

Today's lesson we will devote to solving problems on the topic: “Practical application of triangle similarity " This is a workshop lesson where we will look at the use of similarity features in solving entertaining problems.

Write down the date, class work and topic of the lesson.

III. Updating basic knowledge.

For the lesson to be successful, you need to repeat the theoretical material. But first, let’s check how you have mastered the homework material.

So, I offer you a small test for 3-5 minutes.

a) Testing on the topic “Signs of similarity of triangles”

b) Repetition of theoretical material:

Now please answer my questions:

What triangles are called similar?

Which sides of triangles are called similar?

What is similarity coefficient? (number k equal to the ratio of similar sides)

What are the signs of similarity of triangles?

What is the ratio of the areas of two similar triangles?

c) Oral problem solving:

- Name similar triangles. In what ways are they similar?

-Name the properties of similar triangles

IV. Psychological relief

V. Solving entertaining problems.

Geometry is not just the science of the properties of triangles, parallelograms, and circles. Geometry is a whole world that surrounds us from birth. After all, everything we see around us relates to geometry in one way or another, nothing escapes its attentive gaze. Geometry helps a person walk through the world with his eyes wide open, teaches him to look carefully around and see the beauty of ordinary things, to look and think, to think and draw conclusions.

Geometry is one of the most ancient sciences. It arose on the basis practical activities people and at the beginning of its development served mainly practical purposes. Subsequently, geometry was formed as an independent science that deals with the study of geometric figures.

While studying geometry, you became familiar with similar figures. Today we will discuss how the properties of such triangles can be used to carry out various field measurements. Let's consider the tasks:

determining the height of an object; determining the distance to an inaccessible object

And now I want to offer you an old problem.

Problem 1 . The Greek sage Thales determined the height of the pyramid in Egypt six centuries BC. He took advantage of her shadow. The priests and the pharaoh, gathered at the foot of the highest pyramid, looked with puzzlement at the northern newcomer, who guessed the height of the huge structure.
Thales, says legend, chose the day and hour when the length of his own shadow was equal to his height; at this moment, the height of the pyramid should also be equal to the length of the shadow cast by it. Of course, the length of the shadow had to be
count from the midpoint of the square base of the pyramid; Thales could measure the width of this base directly.

So, Thales taught the Egyptians to determine the height of a pyramid by the length of its shadow:

How this was done is clear from the picture.

He measured the shadow of the stick and the shadow of the pyramid. By comparing the ratios of the heights of real objects with the lengths of their shadows, Thales found the height of the pyramid

Let's change this method so that on a sunny day you can use any shadow, no matter how long it is. Let the pole be 1m long and its shadow 1.2m. Find the height of the tree ifits shadow is 6m.

AB is the length of the stick,DE– height of the pyramid.

 ABC is similar INDE(at two corners):

 SVA= INED=90°;

 DIA = DBE, because corresponding to AS||DB and secant NE (sun rays fall parallel)

;
.

Thus, Thales found the height of the pyramid.

However, the method proposed by Thales is not always applicable. Why?

Determining the height of an object.

There are a few simple ways determining the height of objects. For example, such methods are given in the hunter-sportsman's handbook.

Slide 6

By the shadow . On a sunny day, it is not difficult to measure the height of an object, say a tree, by its shadow. You just need to be guided the following rule: the height of the tree being measured is as many times greater than the height of the object you know (for example, a stick or a gun), how many times the shadow of the tree is greater than the shadow of the stick. If, in our measurement, the shadow of a gun or stick is twice the length of the gun or stick, then the height of the tree will be half the length of its shadow. In the same case, when the shadow of a gun or stick is equal to its length, the height of the tree is also equal to its shadow.

Problem 2. Sherlock Holmes

Along the pole . This method can be used when there is no sun and shadows from objects are not visible. To measure, you need to take a pole equal in length to your height. This pole must be installed at such a distance from the tree that when lying down you can see the top of the tree in a straight line with top point pole Then the height of the tree will be equal to the line drawn from your head to the base of the tree.

Task 3. The next one is also very easy way measurements of tall objects are picturesquely described in Jules Verne's famous novel"Mysterious Island" . Has anyone read this novel?

…Taking a straight pole, 12 feet long, the engineer measured it as accurately as possible, comparing it with his own height, which was well known to him. Not reaching 500 feet from the granite wall, which rose vertically, the engineer stuck a pole about two feet into the sand and, having firmly strengthened it, set it vertically with the help of a plumb line.
Then he moved away from the pole to such a distance that, lying on the sand, he could see both the end of the pole and the edge of the ridge on the same straight line. He carefully marked this point with a peg

– Are you familiar with the rudiments of geometry? – he asked Herbert, rising from the ground.
-Yes
– Do you remember the properties of similar triangles?
– Their similar sides are proportional.
- Right. So: now I will build two similar right triangle. The smaller one will have a vertical pole on one leg, and the distance from the peg to the base of the pole on the other; The hypotenuse is my line of sight. The legs of another triangle will be: a vertical wall, the height of which we want to determine, and the distance from the peg to the base of this wall; the hypotenuse is my line of sight coinciding with the direction of the hypotenuse of the first triangle....”

So the length of the pole is 10 feet (ft = 30 cm). The distance from peg to pole is 15 feet, from wall to pole 500 feet. Find the height of the rock

Interesting tasks? There are a lot of such beautiful problems that can be solved using similarity features.

Solution to problem No. 579,

Determining the height of an object through a puddle . This method can be successfully used after rain, when many puddles appear on the ground. The measurement is carried out in this way: find a puddle not far from the object being measured and stand near it so that it fits between you and the object. After this, a point is found from which the top of the object reflected in the water is visible. The object being measured, for example a tree, will be as many times taller than you as the distance from it to the puddle is greater than the distance from the puddle to you.

Instead of a puddle, you can use a mirror placed horizontally eat. The mirror is placedhorizontally and move back from it to a point where, standing at which, the observer sees the top of the tree in the mirror. A ray of lightFD, reflected from the mirror at a pointD, gets into the human eye.

 ABDsimilar EFD(at two corners):

 VAD=  FED=90°;

 ADB = EDF, because angle of incidence equal to angle reflections.

In similar triangles, similar sides are proportional:

;
.

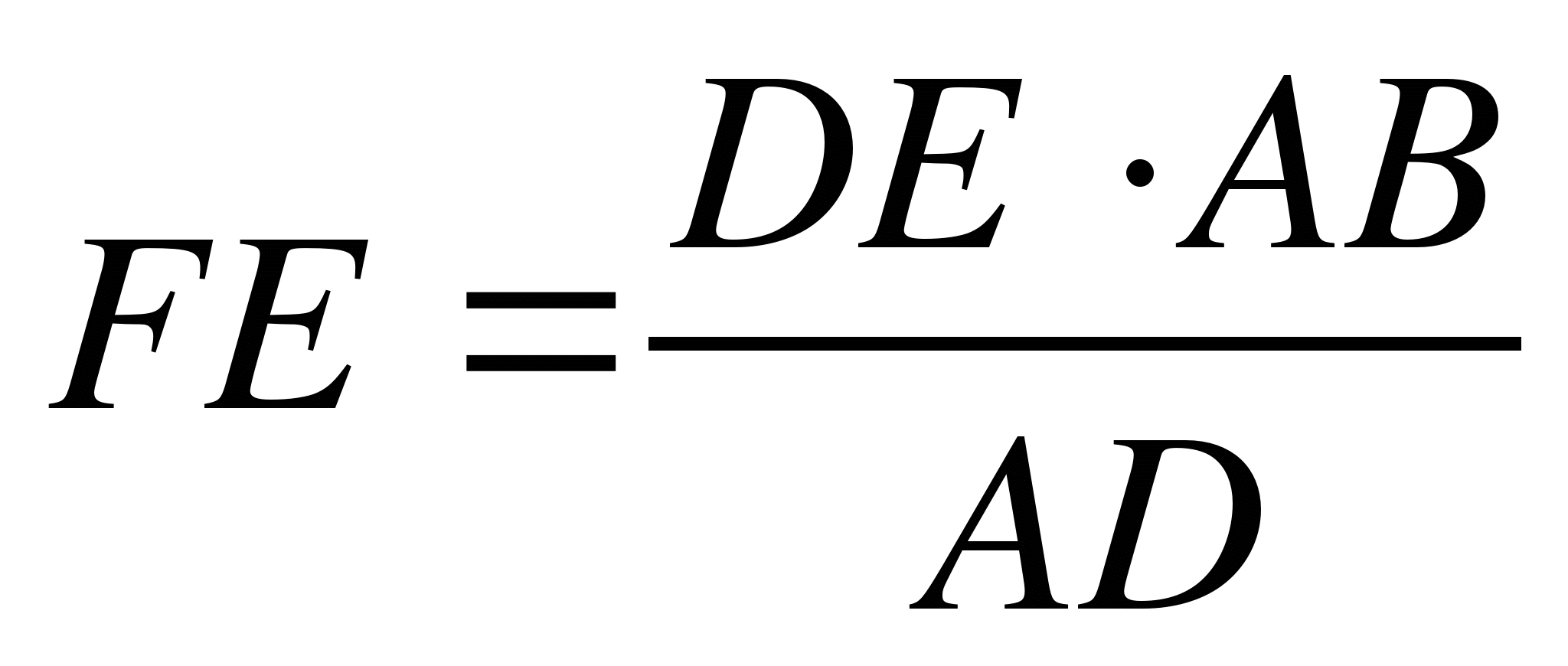Thus, the height of the object is found.

Determining the height of an object using a mirror . №581

Work on the ground

Additional material. 7.1. To “carry out” long sections on the ground, a technique calledhanging straight. This technique is as follows:

First, some points A and B are marked. For this purpose, two milestones are used - poles about 2 m long, pointed at one end so that they can be stuck into the ground. The third milestone (point C) is placed so that the milestones standing at points A and B cover it from the observer located at point A. The next milestone is placed so that it is covered by the milestones standing at points B and C, etc.

7.2. Measuring angles on the ground is carried out using special devices. The simplest of them isastrolabe. The astrolabe consists of two parts: a disk divided into degrees, and a ruler (alidade) rotating around the center of the disk. At the ends of the alidade there are two narrow windows, which are used to position it in a certain direction.

In order to measure AOB on the ground, a tripod with an astrolabe is placed so that the plumb line suspended from the center of the disk is located exactly above point O. Then an alidade is installed along one of the sides OA or OB, and the division opposite which the alidade indicator is located is noted. Next, turn the alidade, directing it along the other side of the measured angle, and mark the division opposite which the alidade pointer will be. The difference in reading gives the degree measure AOB.

Measuring angles on the ground is carried out using special instruments.

Lumberjack Rule

Determining the distance to an inaccessible point

First, you need to remember how long straight lines are drawn on the ground and angles are measured.

hanging straight .

astrolabe .

Slide 11

 A and C. They build on a sheet of paper A 1 IN 1 WITH 1 , which one A= A 1 And C= WITH 1 1 IN 1 and A 1 WITH 1 .

By construction ABC is similar A 1 IN 1 WITH 1 (at two corners).

1) To “carry out” long sections on the ground, use a technique calledhanging straight .

Measuring angles on the ground can be carried out using a special device -astrolabe .

Slide 11

Suppose that you need to find the distance from point A to an inaccessible object B. To do this, select a point C on the ground, draw a segment AC and measure it. Then, using an astrolabe, measure A and C. They build on a sheet of paper A 1 IN 1 WITH 1 , which one A= A 1 And C= WITH 1 . Next, measure the lengths of the sides A 1 ;
.

Thus, the distance to the inaccessible point has been found

Solving problems No. 582,

№583 . Practical task.

It is proposed that, working in pairs, solve problem No. 583.

It proposes, using the similarity of triangles, to measure the width of the river.

The drawing for the problem is in the textbook. You need to explain how such a drawing was obtained, prove the similarity of the triangles and carry out calculations.

Slide 12

V. Independent work in groups

Tasks 1,2,3,4 slide(33-36)

VI. Homework:

P.64, No. 580,582

VI. Lesson summary. Ratings.

– What new did you learn today?

Today in the lesson you worked with the simplest geometric figure, called the “geometry cell”, Solving various tasks By using signs of similarity of triangles, you learned to think correctly logically, compare, generalize, and draw conclusions, thereby developing your mental abilities.

2.

The mean line theorem.

Dad’s felt boots and yours;….

(continue).

In life we ​​speak of similar objects, but in geometry we speak of similar objects. This means that our theory can be applied to these subjects. Let's look at the theory of similarity of triangles in the world around us.

Let's formulate the topic of the lesson.

Work in pairs:

TO

A Is it true that: ?ABC ∞ ?A1B1C1, if ∠A = 46° ∠B = 64° ∠A1 = 46° ∠C1 = 70°

L Is it true that: ?ABC ∞ ?A1B1C1, if AB=13m A1B1=58m P?ABC =25m, then P?A1B1C1 =100m

b Is it true that: ?ABC ∞ ?A1B1C1, if AB=15m A1B1=45m S?A1B1C1 =27 m2, then S?ABC =100m2

TO

L

F

A Is it true that if, then

Check: What word did you get? - “Alpha”.

* A little information:

• In our solar system 1 star is the sun.
• Stars - in the constellation, the most bright Star in the constellation is called "Alpha".
• Stars are objects beyond our reach, but they are studied and the distance to them is found.

And how to do it?

Determining the distance to an inaccessible point. Let's assume that we need to find the distance from point A to an inaccessible point B. To do this, select point C on the ground, draw a segment AC and measure it. Then, using an astrolabe, we measure the angles ∠A and ∠C. On a piece of paper we build some triangle?A1B1C1, in which ∠A1=∠A, ∠C1=∠C, and measure the lengths of the sides A1B1 and A1C1 of this triangle.

Since?ABC ∞ ?A1B1C1, then =, whence. Using the known distances AC, A1C1 and A1B1, we find the distance AB.

To simplify calculations, it is convenient to construct a triangle?A1B1C1 so that A1C1: AC = 1:1000. For example, if AC = 130m, then take the distance A1C1 equal to 130mm. In this case = 1000, therefore, by measuring the distance A1B1 in millimeters, we immediately obtain the distance AB in meters.

Example. Let AC = 130m, ∠A = 73° and ∠C = 58°. On paper we construct a triangle?A1B1C1 so that ∠A1 = 73° and ∠С1 = 58°, A1C1 = 130mm, and measure the segment A1B1. It is equal to 153mm, so the required distance is 153m.

4.

The priest continued arrogantly:

CAB ∞ ?BDE (at 2 angles)

• C = ∠B (by condition)
• B = ∠E = 90°

Answer: 146 m.

AB=2.1 m AE=6.3 m CB=1.7 m

1. Triangles are similar at 2 angles.

ABC ∞ ?AED (at 2 angles)

• A - general
• B = ∠E = 90°

Answer: 5.1 m.

Pa example:

Oh! Tired

Barely keeping up with the teacher

View document contents
“Summary of a geometry lesson on the topic “Practical applications of similarity of triangles.” »

Municipal educational institution

"Naval Cadet School named after. Admiral P. G. Kotov."

Geometry lesson (8th grade)

Topic: “Practical applications of triangle similarity.”

Skirmant Natalya Rudolfovna

higher mathematics teacher

Business address:

164520, Arkhangelsk region,

Severodvinsk, st. Komsomolskaya, 7,

work phone 55-20-86

Severodvinsk

Goals and objectives of the lesson:

show the use of similarity of triangles when carrying out measuring work on the ground;

show the relationship between theory and practice;

introduce students to different ways determining the height of an object and the distance to an inaccessible object;

to develop the ability to apply acquired knowledge when solving various problems of this type.

Developmental

increase students' interest in studying geometry;

intensify cognitive activity students;

to form the qualities of thinking characteristic of mathematical activity and necessary for a productive life in society.

Educational

motivate students' interest in the subject by involving them in solving practical problems.

During the classes:

1.Checking homework.

2. Test “Is it true...” (work in pairs) - repetition of the theory.

3. Task No. 1. Determining the distance to an inaccessible point (completing notes in notebooks with the teacher).

4. Task No. 2. Determining the height of an object:

A). along the length of its shadow (disassemble by ready-made solution in the textbook, prepare option 1 in your notebooks yourself).

b). on a pole (disassemble according to the ready-made solution in the textbook, draw up option 2 in your notebooks yourself).

V). using a mirror (offer to analyze problem No. 581).

5. Lesson results, homework No. 581,583.

1. Checking homework. Explanation of ready-made solution No. 550(1).

Given: drawing.

Triangles are similar at 2 angles.

∆BAD ∞ ∆KCB (at 2 angles)

∠B = ∠K (by condition)

∠A = ∠C = 90°

2. Teacher: “Guys, we have studied the entire theory of similarity of triangles.”

We considered the use of similarity in proving theorems.

What theorems have we proven?

The mean line theorem.

Property of medians of a triangle.

IN Everyday life We are surrounded by objects of the same shape.

Example: - tennis and soccer ball;

Dad’s felt boots and yours;….

(continue).

In life we ​​speak of similar objects, but in geometry we speak of similar objects. This means that our theory can be applied to these subjects. Let's look at the theory of similarity of triangles in the world around us.

Let's formulate the topic of the lesson.

Students: “Practical applications of similarity of triangles.”

Teacher: “In order to apply a theory, we must know it well. Let's repeat:

Work in pairs:

Is this statement true? If true, leave the letter before the statement, otherwise cross it out.

Test “Is it true...” (work in pairs) - repetition of the theory.

TO Is it true that: in similar triangles, similar sides are equal.

A Is it true that: ∆ABC ∞ ∆A 1 B 1 C 1 if ∠A = 46° ∠B = 64° ∠A1 = 46° ∠C1 = 70°

L Is it true that: ∆ABC ∞ ∆A 1 B 1 C 1, if AB=13m A1B1=58m P ∆ ABC =25m, then P ∆ A 1 B 1 C 1 =100m

b Is it true that: ∆ABC ∞ ∆A1B1C1, if AB=15m A1B1=45m S ∆ A 1 B 1 C 1 =27 m 2, then S ∆ ABC =100m 2

TO Is it true that: in similar triangles the corresponding angles are proportional

L Is it true (a brief statement of the criterion for the similarity of triangles) “Triangles are similar at three angles”

F Is it true (a brief statement of the criterion for the similarity of triangles) “Triangles are similar in two proportional sides and the angle between them”

A Is it true that if, then

Check: What word did you get? - “Alpha”.

* A little information:

• In our solar system, 1 star is the sun.

  All other stars are outside our solar system.

  Stars are in a constellation, the brightest star in the constellation is called “Alpha”.

  Stars are objects beyond our reach, but they are studied and the distance to them is found.

And how to do it?

3. Task No. 1. Determining the distance to an inaccessible point (completing notes in notebooks with the teacher).

Determining the distance to an inaccessible point. Let's assume that we need to find the distance from point A to an inaccessible point B. To do this, select point C on the ground, draw a segment AC and measure it. Then, using an astrolabe, we measure the angles ∠A and ∠C. On a piece of paper we build some triangle ∆A 1 B 1 C 1, in which ∠A 1 =∠A, ∠C 1 =∠C, and measure the lengths of the sides A 1 B 1 and A 1 C 1 of this triangle.

Since ∆ABC ∞ ∆A 1 B 1 C 1 , then = , whence. Using the known distances AC, A 1 C 1 and A 1 B 1, we find the distance AB.

To simplify calculations, it is convenient to construct a triangle ∆A 1 B 1 C 1 so that A 1 C 1: AC = 1:1000. For example, if AC = 130m, then take the distance A 1 C 1 equal to 130mm. In this case = 1000, therefore, by measuring the distance A 1 B 1 in millimeters, we immediately obtain the distance AB in meters.

Example. Let AC = 130m, ∠A = 73° and ∠C = 58°. On paper we construct a triangle ∆A 1 B 1 C 1 so that ∠A 1 = 73° and ∠C 1 = 58°, A 1 C 1 = 130mm, and measure the segment A 1 B 1. It is equal to 153mm, so the required distance is 153m.

4. Teacher: Let's return to earthly affairs. Greek scientists solved many practical problems that they had not been able to solve before. For example, six centuries BC, the Greek sage Thales of Miletus taught the Egyptians to determine the height of a pyramid by the length of its shadow.

How it happened is described in the book by Ya.I. Perelman "Entertaining Geometry". Thales, says legend, chose the day and hour when the length of his own shadow was equal to his height; at this moment the height of the pyramid must also be equal to the length of the shadow it casts. This is, perhaps, the only case when a person benefited from his shadow. Let's listen to the parable. (one of the students says).

“A tired northern stranger came to the country of the Great Hapi. The sun was already setting when he approached the magnificent palace of the pharaoh and said something to the servants. They instantly opened the doors for him and led him into the reception hall. And here he stands in a dusty field cloak, and in front of him sits the pharaoh on a gilded throne. Next to him stand arrogant priests, guardians of the eternal secrets of nature.

Who are you? - asked the high priest.

My name is Thales. I am originally from Miletus.

The priest continued arrogantly:

So you were the one who boasted that you could measure the height of the pyramid without climbing it? - the priests bent over with laughter.

It will be good,” the priest continued mockingly, “if you are mistaken by no more than a hundred cubits.”

I can measure the height of the pyramid and be off by no more than half a cubit. I'll do it tomorrow.

The priests' faces darkened. What a cheek! This stranger claims that he can figure out what they, the priests of Great Egypt, cannot.

Okay, said Pharaoh. - There is a pyramid near the palace, we know its height. Tomorrow we'll check your art."

The next day, Thales found a long stick and stuck it into the ground a little further from the pyramid. I waited certain moment. He measured the shadow of the stick and the shadow of the pyramid. By comparing the ratios of the heights of real objects with the lengths of their shadows, Thales found the height of the pyramid.

Task No. 2. Determining the height of an object:

A). along the length of its shadow (look at the ready-made solution in the textbook, draw up option 1 in your notebooks yourself).

CB=8.4 m BE=1022 m AB=1.2 m ∠C = ∠B

Triangles are similar at 2 angles.

∆CAB ∞ ∆BDE (at 2 angles)

∠C = ∠B (by condition)

∠B = ∠E = 90°

Answer: 146 m.

b). on a pole (disassemble according to the ready-made solution in the textbook, draw up option 2 in your notebooks yourself).

AB=2.1 m AE=6.3 m CB=1.7 m

Triangles are similar at 2 angles.

∆ABC ∞ ∆AED (at 2 angles)

∠A - general

∠B = ∠E = 90°

Answer: 5.1 m.

V). using a mirror (offer to analyze problem No. 581 (D/z)).

To determine the height of the tree, you can use a mirror as shown in the figure. A ray of light FD, reflected from the mirror at point D, enters the human eye (point B). Determine the height of the tree if AC=165 cm, BC=12 cm, AD=120 cm, DE=4.8 m, ∠1 = ∠2.

5. Teacher: Let’s summarize the lesson:

Today in class we learned about different ways to measure the height of an object; distance to an inaccessible point; applied the theory of similarity.

Formulate your attitude to the lesson in a sentence or phrase, starting it with the letter included in the word “similarity”

Pa example:

Oh! Tired

Barely keeping up with the teacher

Lesson summary

Municipal budgetary educational institution

"Pizhemskaya secondary school"

Geometry lesson in 8th grade on the topic:

"Practical Applications

similarities of triangles"
Author
: Rubtsova Lyubov Grigorievna,
mathematic teacher, highest category, work experience 33 years, 2016 Lesson topic:
“Application of triangle similarity to solving practical problems”
Target:
organize students’ activities to perceive, comprehend and consolidate new knowledge and methods of activity on the topic being studied.
Tasks:
- educational (formation of cognitive learning tools): teach to use the signs of similarity of triangles, the properties of similar triangles when solving practical problems, - educational (formation of communicative and personal learning skills): develop the ability to listen and engage in dialogue, participate in a collective discussion of problems, cultivate responsibility and accuracy , - developing (formation of regulatory UUD) to form the communicative competence of students; choose methods for solving problems depending on specific conditions; reflection on methods and conditions of action, control and evaluation of the process and results of activity. Equipment: projector, laptop, interactive whiteboard, handouts, presentation.
Lesson Plan
1. Organizational moment 2. Updating of students’ acquired knowledge of learning activities 3. Formulation of the topic and objectives of the lesson 4. Application theoretical foundations when solving practical problems 5. Physical education lesson 6. Reinforcement of material 7. Application of theoretical foundations in constructing the Sierpinski triangle 8. Summing up. Reflection
1. Organizational moment (3 min)
Hello guys! Let me start the lesson with the words of the French mathematician, philosopher, and physicist R. Descartes: “The curious seeks joy only so that it
to be surprised, but the inquisitive is to recognize them and stop being surprised.” So let's be inquisitive in class today.
2.Updating knowledge - (5 min)
Geometry is one of the most ancient sciences. Translated from Greek, the word “geometry” means “land surveying”. This name is associated with various measuring works. Thus, geometry arose on the basis of the practical activities of people, and later formed as an independent science engaged in the study of geometric figures.
1
(Work in groups).
2
Help each other remember the definition of similar triangles (two triangles are called similar if their angles are respectively equal and the sides of one triangle are proportional to similar sides of the other triangle), signs of similarity (
3
sign: if two angles of one triangle are respectively equal to two angles of another, then such triangles are similar,
sign: if two sides of one triangle are proportional to two sides of another triangle and the angles between these sides are equal, then such triangles are similar,
sign: if the three sides of one triangle are proportional to the three sides of another triangle, then such triangles are similar). Properties of similar triangles associated with the ratio of the perimeters and the ratio of the areas of similar triangles (the ratio of the areas of similar triangles is equal to the square of the similarity coefficient. The ratio of the perimeters of similar triangles is equal to the similarity coefficient) . Guys, take the “Worksheets” (Appendix 1,2,3) and sign them.
Test for establishing the truth and falsity of statements
1. Two triangles are similar if their angles are respectively equal and similar sides are proportional. (Yes)
We remembered the properties and signs of similarity of triangles. Where do you think this theoretical knowledge can be applied? (on practice). What is the topic of the lesson? ( practical use similarity of triangles). Formulate the purpose of the lesson (consider cases of using the similarity of triangles, consolidate knowledge when solving problems). Write down the topic of the lesson on the Worksheets. Pay attention to the objects: a matryoshka doll and two books. Think about what they have to do with our lesson? Answer at the end of the lesson.
4.Learning new material (10 min)
The idea of ​​ratio and proportion originated in ancient times. Figures of the same shape, but different in size, are found back in the 3rd millennium BC. This is evidenced by ancient Greek temples, palaces and many other ancient monuments.
The idea of ​​similarity developed in various countries in parallel and arose from the need to solve problems of determining the size of inaccessible objects. The first to determine the height of the unattainable body was Thales of Miletus. He determined the height of the pyramid by the shadow cast by the pyramid. How is this possible, and what methods of determining the size of bodies are found in history? Now we will work in groups (1st row, 2nd row, 3rd row). You need to become familiar with some ways to determine the size of bodies. (children get acquainted with the methods of determining geometrically the sizes of bodies through similar triangles - 3 min)
1 group.

Determining body height by shadow
On a sunny day, it is not difficult to measure the height of an object, say a tree, by its shadow. It is only necessary to take an object (for example, a stick) of a known length and place it perpendicular to the surface. Then a shadow will fall from the object. Knowing the height of the stick, the length of the shadow from the stick, the length of the shadow from the object whose height we are measuring, we can determine the height of the object. To do this we need to consider the similarity
two triangles. Remember: the sun's rays fall parallel to each other.
2nd group

Determining body height using a pole
This method was specifically described by Jules Verne in the novel “The Mysterious Island”. This method can be used when there is no sun and shadows from objects are not visible. To measure, you need to take a pole equal in length to your height. This pole must be installed at such a distance from the object that when lying down you can see the top of the object in a straight line with the top point of the pole. Then the height of the object can be found by knowing the length of the line drawn from your head to the base of the object.
3 group

Determining body height using a mirror
The mirror is placed horizontally and moved back from it to a point where, standing at which, the observer sees the top of a tree in the mirror. A ray of light FD, reflected from a mirror at point D, enters the human eye. The object being measured, for example a tree, will be as many times taller than you as the distance from it to the mirror is greater than the distance from the mirror to you. Remember: the angle of incidence is equal to the angle of reflection (law of reflection). Let's see what we got? One person from the group comes to the board and demonstrates the methods, everyone else listens carefully and records the material in the “Worksheets”
5. Physical education for the eyes: (2 min)
Draw a triangle with your eyes. Now turn it over, top down. And again, guide the perimeter with your eyes. Draw a figure eight vertically. Don't turn your head, Just be careful with your eyes along the lines of the water. And put it on the side. Now follow horizontally, and stop in the center. Close your eyes tightly, don't be lazy. We finally open our eyes. Charging has ended. Each of you is great!

6.Secure the material
.(
10 min)
Solving problems Problems are solved independently using the options on the “Worksheets”, then one student comes to the board with a ready-made solution. I option. 1. A tree 1 m high is 8 steps from a lamppost and casts a shadow 4 steps long. Determine the height of the lamp post. (Complete the drawing for the problem) Option II.
№1.
The short arm of the barrier is 60cm long, and the long arm is 240cm. To what height does the end of the long arm rise when the end of the short arm descends 30 cm? III option.1. The length of the shadow of the factory chimney is 24 m; the height of the pipe is 50 m, at the same time, a pole stuck vertically into the ground gives a shadow 1 m long. Find the length of the pole. (Complete the drawing for the problem) Evaluate yourself. Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made. Let's compare the answers: Option 1 (3m); Option 2 (120cm), Option 3 (2 m) 7.
Application of theoretical foundations when constructing a triangle

Sierpinski.(8 min)
Now let’s complete the task in the “Worksheets” - the Sierpinski triangle. To do this, divide equilateral triangle with the side
A
into 4 equal triangles. (Think about how to do this). Color the central triangle red. Then divide the 3 triangles again into 4 equal triangles. Color each central one blue. Find the similarity coefficients of triangles using the options (option 1:
largest to red), option 2: red triangle to blue, option 3: red triangle to blue). Consider the triangles: Option 1: the largest and red triangles (remember that you drew the middle lines). On what basis are the triangles similar? _____ Option 2: red and blue triangles (remember that you drew the middle lines). On what basis are the triangles similar? _____ Option 1: the largest and red triangles (remember that you drew the middle lines). On what basis are the triangles similar? _____ Similarity coefficient of large triangle and blue triangle = ________ Similarity coefficient of blue triangle and red triangle = ____________ Similarity coefficient of large triangle and blue triangle = ________ What values ​​did you get for the similarity coefficient? (K=2). So, we get a very interesting figure, which is called self-similar. The French mathematician Mandelbrot called figures, each element of which is similar to itself, fractals. There are fractals created by scientists and created by nature.
French mathematician Mandelbrot The simplest example of a fractal is a nesting doll. Examples of fractals (Appendix 4) Evaluate yourself. Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made.
8.Lesson summary (5 min)
-What do you remember most about the lesson?
№1.
- “I remember that...” - What surprised you? “It turns out that...” -What did you like most? “I liked it...” Yes, indeed, knowing the laws of geometry, we discovered a lot for ourselves. Homework:
№2.
A 15 m high pillar is covered by a coin with a diameter of 2 cm if held at a distance of 70 cm from the eyes. Find the distance from the pillar to the observer.
A tennis ball is served from a height of 2 m 10 cm and flies over the net itself, height 90 cm. At what distance from the net will the ball hit the ground if it is served from the line, located 12 m from the net, and flies in a straight line? And in conclusion, I would like to say: geometry is not a fully understood science, and perhaps many discoveries await precisely you. I wish you good luck in your further study of geometry!
Annex 1

Worksheet
Full name________________________________________________
1 group
Check your answer with the board and evaluate yourself. Evaluation criteria: “5” - no errors, “4” - 1 or 2 errors, “3” - 3 or 4 errors, “!” - more than 4 errors. We assign grades immediately on the “Worksheet”. _________ Lesson topic:___________________________________________________________ _____________________________________________________________________
Task 2. Determining the height of a body from the shadow (group work)
On a sunny day, it is not difficult to measure the height of an object, say a tree, by its shadow. It is only necessary to take an object (for example, a stick) of a known length and place it perpendicular to the surface. Then a shadow will fall from the object. Knowing the height of the stick, the length of the shadow from the stick, the length of the shadow from the object whose height we are measuring, we can determine the height of the object. To do this, you need to consider the similarity of two triangles. Remember: the sun's rays fall parallel to each other.

Task 3. Fastening the material

Solve problems.
Problem 1. A tree 1 m high is located 8 steps from a lamppost and casts a shadow 4 steps long. Determine the height of the lamp post. (Make a drawing for the problem) Solution: _____ Task 2. (Orally) Analyze the solution to the problem and find the error (problem on the board) Evaluate yourself. Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors.
Task 4. Application of theoretical foundations when constructing a triangle

Sierpinski
. Solution

A
into 4 equal triangles. Color the central one red. Then divide the 3 triangles again into 4 equal triangles. Color each central one blue. Prove that the blue and red triangles are similar. Find the similarity coefficient of these triangles. Evaluate yourself.
Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors. _____

Final grade ________

№1.

№2.
Homework:
Annex 1

A tennis ball is served from a height of 2 m 10 cm and flies over the net itself, height 90 cm. At what distance from the net will the ball hit the ground if it is served from the line, located 12 m from the net, and flies in a straight line Appendix 2

2nd group

Full name_____________________________________________
Check your answer with the board and evaluate yourself. Evaluation criteria: “5” - no errors, “4” - 1 or 2 errors, “3” - 3 or 4 errors, “!” - more than 4 errors. We assign grades immediately on the “Worksheet”. ____ Lesson topic:_________________________________________________________________ _____________________________________________________________________
Task 2. Determining body height using a pole (group work)
This method was specifically described by Jules Verne in the novel “The Mysterious Island”. This method can be used when there is no sun and shadows from objects are not visible. To measure, you need to take a pole equal in length to your height. You need this pole
install at such a distance from the object that when lying down you can see the top of the object in one straight line with the top point of the pole. Then the height of the object can be found by knowing the length of the line drawn from your head to the base of the object.

№1.
The short arm of the barrier is 60cm long, and the long arm is 240cm. To what height does the end of the long arm rise when the end of the short arm descends 30 cm? Solution: ______ Task 2. (Oral) Analyze the solution to the problem and find the error (task on the board) Check the answer with the board and evaluate yourself. Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors.

Sierpinski

Solution:
Divide an equilateral triangle with side
A
into 4 equal triangles. Color the central one red. Then divide the 3 triangles again into 4 equal triangles. Color each central one blue. Prove that the big and red triangles are similar. Find the similarity coefficient of these triangles. Evaluate yourself. Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors.
Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors. _____

(arithmetic mean of three estimates)

Homework (solve 2 problems to choose from)

№1.
A 15 m high pillar is covered by a coin with a diameter of 2 cm if held at a distance of 70 cm from the eyes. Find the distance from the pillar to the observer.
№2.
A tennis ball is served from a height of 2 m 10 cm and flies over the net itself, height 90 cm. At what distance from the net will the ball hit the ground if it is served from the line, located 12 m from the net, and flies in a straight line Appendix 3
Annex 1

Full name________________________________________________

3 group

Task 1. Test to determine the truth and falsity of statements
Check your answer with the board and evaluate yourself. Evaluation criteria: “5” - no errors, “4” - 1 or 2 errors, “3” - 3 or 4 errors, “!” - more than 4 errors. The grades are given immediately on the “Worksheet”. ___ Lesson topic:_________________________________________________________________ _____________________________________________________________________

Task 2. Determining body height using a mirror (group work)
The mirror is placed horizontally and moved back from it to a point where, standing at which, the observer sees the top of a tree in the mirror. A ray of light FD, reflected from a mirror at point D, enters the human eye. The object being measured, for example a tree, will be as many times taller than you as the distance from it to the mirror is greater than the distance from the mirror to you. Remember: the angle of incidence is equal to the angle of reflection (law of reflection).
Task 3. Fastening the material
The length of the shadow of the factory chimney is 24 m; the height of the pipe is 50 m, at the same time, a pole vertically stuck into the ground gives a shadow 2 m long. Find the length of the pole. (Make a drawing for the problem) Solution: _____ Problem 2. (Oral) Analyze the solution to the problem and find the error (problem on the board) Answer check with the board and evaluate yourself.
Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors.

Task 4 Application of theoretical foundations when constructing a triangle

Solution:
Divide an equilateral triangle with side
A
Sierpinski.
Evaluation criteria: “5” - completed without errors, “4” - one error was made, “3” - more than one error was made, “!” - more than 4 errors. _____

(arithmetic mean of three estimates)

№1.
A 15 m high pillar is covered by a coin with a diameter of 2 cm if held at a distance of 70 cm from the eyes. Find the distance from the pillar to the observer.
№2.
into 4 equal triangles. Color the central one red. Then divide the 3 triangles again into 4 equal triangles. Color each central one blue. Prove that the big and red triangles are similar. Find the similarity coefficient of these triangles. Rate yourself