5 komplekse tall. Opplæring: komplekse tall
Komplekse tall
Innbilt og komplekse tall. Abscisse og ordinat
komplekst tall. Konjuger komplekse tall.
Operasjoner med komplekse tall. Geometrisk
representasjon av komplekse tall. komplekst plan.
Modul og argument for et komplekst tall. trigonometrisk
kompleks tallform. Operasjoner med kompleks
tall i trigonometrisk form. Moivre formel.
Grunnleggende informasjon om innbilt og komplekse tall er gitt i avsnittet "imaginære og komplekse tall". Behovet for disse tallene av en ny type dukket opp ved løsning av kvadratiske ligninger for tilfellet
D< 0 (здесь Der diskriminanten til den kvadratiske ligningen). I lang tid fant ikke disse tallene fysisk bruk, og derfor ble de kalt «imaginære» tall. Imidlertid er de nå veldig mye brukt i ulike felt av fysikk.og teknologi: elektroteknikk, hydro- og aerodynamikk, teorien om elastisitet, etc.
Komplekse tall er skrevet som:a+bi. Her en og b – reelle tall , a Jeg – imaginær enhet. e. Jeg 2 = –1. Antall en kalt abscisse, a b - ordinatkomplekst talla + b.To komplekse talla+bi og a-bi kalt konjugerer komplekse tall.
Hovedavtaler:
1. Reelt tall
enkan også skrives i skjemaetkomplekst tall:et + 0 Jeg eller en - 0 Jeg. For eksempel oppføringer 5 + 0Jeg og 5-0 Jegbetyr samme tall 5 .2. Kompleks tall 0 + bikalt rent innbilt Antall. Innspillingbibetyr det samme som 0 + bi.
3. To komplekse talla+bi ogc + dianses like hvisa = c og b = d. Ellers komplekse tall er ikke like.
Addisjon. Summen av komplekse talla+bi og c + dikalles et komplekst tall (a+c ) + (b+d ) Jeg .På denne måten, når det legges til komplekse tall, deres abscisse og ordinater legges til separat.
Denne definisjonen følger reglene for håndtering av vanlige polynomer.
Subtraksjon. Forskjellen mellom to komplekse talla+bi(redusert) og c + di(trukket fra) kalles et komplekst tall (a-c ) + (b-d ) Jeg .
På denne måten, når du trekker fra to komplekse tall, trekkes abscissene og ordinatene deres separat.
Multiplikasjon. Produktet av komplekse talla+bi og c + di kalles et komplekst tall.
(ac-bd ) + (annonse+bc ) Jeg .Denne definisjonen stammer fra to krav:
1) tall a+bi og c + diskal multiplisere som algebraisk binomialer,
2) nummer Jeghar hovedegenskapen:Jeg 2 = – 1.
EKSEMPEL ( a + bi )(a-bi) = a 2 +b 2 . Følgelig arbeid
to konjugerte komplekse tall er lik det reelle
positivt tall.
Inndeling. Del et komplekst talla+bi (delelig) til en annenc + di(deler) - betyr å finne det tredje tallete + fi(chat), som, når multiplisert med en divisorc + di, som resulterer i utbyttea + b.
Hvis divisor ikke er null, er divisjon alltid mulig.
EKSEMPEL Finn (8+Jeg ) : (2 – 3 Jeg) .
Løsning. La oss omskrive dette forholdet som en brøk:
Multipliser telleren og nevneren med 2 + 3Jeg
Og etter å ha utført alle transformasjonene får vi:

Geometrisk representasjon av komplekse tall. Reelle tall er representert med punkter på tallinjen:
Her er poenget ENbetyr nummer -3, prikkB er tallet 2, og O- null. I kontrast er komplekse tall representert av punkter på koordinatplanet. Til dette velger vi rektangulære (kartesiske) koordinater med samme skala på begge akser. Deretter det komplekse talleta+bi vil bli representert med en prikk P med abscisse a og ordinat b (se fig.). Dette koordinatsystemet kalles komplekst plan .

modul komplekst tall kalles lengden på vektorenOP, som viser et komplekst tall på koordinaten ( integrert) fly. Kompleks tallmodula+bi betegnet med | a+bi| eller brev r
For å løse problemer med komplekse tall, må du forstå de grunnleggende definisjonene. Hovedmålet med denne oversiktsartikkelen er å forklare hva komplekse tall er og presentere metoder for å løse grunnleggende problemer med komplekse tall. Dermed er et komplekst tall et tall av formen z = a + bi, hvor a, b- reelle tall, som kalles henholdsvis de reelle og imaginære delene av det komplekse tallet, og betegner a = Re(z), b=Im(z).
Jeg kalles den imaginære enheten. i 2 \u003d -1. Spesielt kan ethvert reelt tall betraktes som komplekst: a = a + 0i, hvor a er ekte. Hvis a = 0 og b ≠ 0, da kalles tallet rent imaginært.
Vi introduserer nå operasjoner på komplekse tall.
Tenk på to komplekse tall z 1 = a 1 + b 1 i og z 2 = a 2 + b 2 i.
Ta i betraktning z = a + bi.

Settet med komplekse tall utvider settet med reelle tall, som igjen utvider settet med rasjonelle tall, og så videre. Denne kjeden av innebygginger kan sees i figuren: N - naturlige tall, Z - heltall, Q - rasjonell, R - reell, C - kompleks. 
Representasjon av komplekse tall
Algebraisk notasjon.
Tenk på et komplekst tall z = a + bi, kalles denne formen for å skrive et komplekst tall algebraisk. Vi har allerede diskutert denne skriveformen i detalj i forrige avsnitt. Bruk ofte følgende illustrative tegning 
trigonometrisk form.
Det kan sees av figuren at tallet z = a + bi kan skrives annerledes. Det er åpenbart det a = rcos(φ), b = rsin(φ), r=|z|, Følgelig z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π)
kalles argumentet til et komplekst tall. Denne representasjonen av et komplekst tall kalles trigonometrisk form. Den trigonometriske formen for notasjon er noen ganger veldig praktisk. For eksempel er det praktisk å bruke det for å heve et komplekst tall til en heltallspotens, nemlig hvis z = rcos(φ) + rsin(φ)i, deretter z n = r n cos(nφ) + r n sin(nφ)i, kalles denne formelen De Moivres formel.
Demonstrativ form.
Ta i betraktning z = rcos(φ) + rsin(φ)i er et komplekst tall i trigonometrisk form, skriver vi det på en annen form z = r(cos(φ) + sin(φ)i) = re iφ, den siste likheten følger av Euler-formelen, så vi fikk en ny form for å skrive et komplekst tall: z = re iφ, som kalles demonstrativt. Denne formen for notasjon er også veldig praktisk for å heve et komplekst tall til en potens: z n = r n e inφ, her n ikke nødvendigvis et heltall, men kan være et vilkårlig reelt tall. Denne skriveformen brukes ganske ofte for å løse problemer.
Grunnleggende teorem for høyere algebra
Tenk deg at vi har en andregradsligning x 2 + x + 1 = 0 . Det er åpenbart at diskriminanten til denne ligningen er negativ og den har ingen reelle røtter, men det viser seg at denne ligningen har to forskjellige komplekse røtter. Så, hovedsetningen til høyere algebra sier at ethvert polynom av grad n har minst en kompleks rot. Det følger av dette at ethvert polynom av grad n har nøyaktig n komplekse røtter, tatt i betraktning deres mangfold. Denne teoremet er et svært viktig resultat i matematikk og er mye brukt. En enkel konsekvens av denne teoremet er at det er nøyaktig n distinkte n-graders røtter til enhet.
Hovedtyper av oppgaver
I denne delen vil hovedtypene av enkle komplekse tallproblemer bli vurdert. Konvensjonelt kan problemer på komplekse tall deles inn i følgende kategorier.
- Utføre enkle aritmetiske operasjoner på komplekse tall.
- Finne røttene til polynomer i komplekse tall.
- Heve komplekse tall til en potens.
- Ekstraksjon av røtter fra komplekse tall.
- Anvendelse av komplekse tall for å løse andre problemer.
Vurder nå de generelle metodene for å løse disse problemene.
De enkleste aritmetiske operasjonene med komplekse tall utføres i henhold til reglene beskrevet i den første delen, men hvis komplekse tall presenteres i trigonometriske eller eksponentielle former, kan de i dette tilfellet konverteres til algebraisk form og utføre operasjoner i henhold til kjente regler.
Å finne røttene til polynomer kommer vanligvis ned til å finne røttene til en kvadratisk ligning. Anta at vi har en kvadratisk ligning, hvis diskriminanten er ikke-negativ, vil røttene være reelle og finnes i henhold til en velkjent formel. Hvis diskriminanten er negativ, da D = -1∙a 2, hvor en er et visst tall, så kan vi representere diskriminanten i skjemaet D = (ia) 2, Følgelig √D = i|a|, og så kan du bruke den allerede kjente formelen for røttene til kvadratisk ligning.
Eksempel. La oss gå tilbake til den andregradsligningen nevnt ovenfor x 2 + x + 1 = 0.
Diskriminerende - D \u003d 1 - 4 ∙ 1 \u003d -3 \u003d -1 (√3) 2 \u003d (i√3) 2.
Nå kan vi enkelt finne røttene: 
Å heve komplekse tall til en potens kan gjøres på flere måter. Hvis du vil heve et komplekst tall i algebraisk form til en liten potens (2 eller 3), kan du gjøre dette ved direkte multiplikasjon, men hvis graden er større (i oppgaver er den ofte mye større), må du skriv dette tallet i trigonometriske eller eksponentielle former og bruk allerede kjente metoder.
Eksempel. Tenk på z = 1 + i og hev til tiende potens.
Vi skriver z i eksponentiell form: z = √2 e iπ/4 .
Deretter z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4.
La oss gå tilbake til den algebraiske formen: z 10 = -32i.
Å trekke ut røtter fra komplekse tall er den inverse operasjonen med hensyn til eksponentiering, så det gjøres på lignende måte. For å trekke ut røttene brukes ofte den eksponentielle formen for å skrive et tall.
Eksempel. Finn alle røttene til grad 3 av enhet. For å gjøre dette finner vi alle røttene til ligningen z 3 = 1, vi vil se etter røttene i eksponentiell form.
Erstatter i ligningen: r 3 e 3iφ = 1 eller r 3 e 3iφ = e 0 .
Derfor: r = 1, 3φ = 0 + 2πk, derav φ = 2πk/3.
Ulike røtter oppnås ved φ = 0, 2π/3, 4π/3.
Derfor er 1 , e i2π/3 , e i4π/3 røtter.
Eller i algebraisk form: 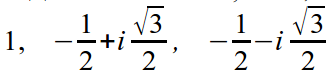
Den siste typen problemer inkluderer et stort utvalg problemer, og det finnes ingen generelle metoder for å løse dem. Her er et enkelt eksempel på en slik oppgave:
Finn beløpet sin(x) + sin(2x) + sin(2x) + … + sin(nx).
Selv om formuleringen av dette problemet ikke refererer til komplekse tall, men med deres hjelp kan det enkelt løses. For å løse det, brukes følgende representasjoner: 
Hvis vi nå erstatter denne representasjonen i summen, reduseres problemet til summeringen av den vanlige geometriske progresjonen.
Konklusjon
Komplekse tall er mye brukt i matematikk, denne oversiktsartikkelen diskuterte de grunnleggende operasjonene på komplekse tall, beskrev flere typer standardproblemer og beskrev kort generelle metoder for å løse dem, for en mer detaljert studie av mulighetene for komplekse tall, anbefales det å bruke spesiallitteratur.
Litteratur
Husk nødvendig informasjon om komplekse tall.
Komplekst tall er et uttrykk for formen en + bi, hvor en, b er reelle tall, og Jeg- såkalte imaginær enhet, symbolet hvis kvadrat er -1, dvs. Jeg 2 = -1. Antall en kalt ekte del, og nummeret b - imaginær del komplekst tall z = en + bi. Hvis en b= 0, så i stedet for en + 0Jeg skriv enkelt en. Man kan se at reelle tall er et spesialtilfelle av komplekse tall.
Aritmetiske operasjoner på komplekse tall er de samme som på reelle: de kan adderes, subtraheres, multipliseres og divideres med hverandre. Addisjon og subtraksjon fortsetter i henhold til regelen ( en + bi) ± ( c + di) = (en ± c) + (b ± d)Jeg, og multiplikasjon - i henhold til regelen ( en + bi) · ( c + di) = (ac – bd) + (annonse + f.Kr)Jeg(her er det bare brukt det Jeg 2 = -1). Tall = en – bi kalt komplekst konjugat til z = en + bi. Likestilling z · = en 2 + b 2 lar deg forstå hvordan du deler et komplekst tall med et annet (ikke-null) komplekst tall:
(For eksempel, ![]() .)
.)

Komplekse tall har en praktisk og visuell geometrisk representasjon: tallet z = en + bi kan representeres som en vektor med koordinater ( en; b) på det kartesiske planet (eller, som er nesten det samme, et punkt - slutten av vektoren med disse koordinatene). I dette tilfellet er summen av to komplekse tall avbildet som summen av de tilsvarende vektorene (som kan finnes av parallellogramregelen). Ved Pythagoras teorem, lengden på vektoren med koordinater ( en; b) er lik . Denne verdien kalles modul komplekst tall z = en + bi og er betegnet med | z|. Vinkelen som denne vektoren lager med den positive retningen til x-aksen (telt mot klokken) kalles argument komplekst tall z og betegnet med Arg z. Argumentet er ikke unikt definert, men bare opp til tillegg av et multiplum av 2 π
radianer (eller 360°, hvis du teller i grader) - det er tross alt klart at det å snu gjennom en slik vinkel rundt origo ikke vil endre vektoren. Men hvis vektoren av lengde r danner en vinkel φ
med den positive retningen til x-aksen, så er dens koordinater lik ( r cos φ
; r synd φ
). Derfor viser det seg trigonometrisk notasjon komplekst tall: z = |z| (cos(Arg z) + Jeg synd (Arg z)). Det er ofte praktisk å skrive komplekse tall i denne formen, fordi det i stor grad forenkler beregninger. Multiplikasjon av komplekse tall i trigonometrisk form ser veldig enkelt ut: z en · z 2 = |z 1 | · | z 2 | (cos(Arg z 1+arg z 2) + Jeg synd (Arg z 1+arg z 2)) (når du multipliserer to komplekse tall, multipliseres modulene deres og argumentene legges til). Herfra følger De Moivre-formler: z n = |z|n(cos( n(Arg z)) + Jeg synd( n(Arg z))). Ved hjelp av disse formlene er det lett å lære å trekke ut røtter av en hvilken som helst grad fra komplekse tall. n-te rot av z er et så komplekst tall w, hva w n = z. Det er klart det ![]() , Og hvor k kan ta hvilken som helst verdi fra settet (0, 1, ..., n- en). Dette betyr at det alltid er nøyaktig n røtter n grad fra et komplekst tall (på planet er de plassert ved toppunktene til en regulær n-gon).
, Og hvor k kan ta hvilken som helst verdi fra settet (0, 1, ..., n- en). Dette betyr at det alltid er nøyaktig n røtter n grad fra et komplekst tall (på planet er de plassert ved toppunktene til en regulær n-gon).
§ 1. Komplekse tall: definisjoner, geometrisk tolkning, operasjoner i algebraiske, trigonometriske og eksponentielle former
Definisjon av et komplekst tall
Komplekse likheter
Geometrisk representasjon av komplekse tall
Modul og argument for et komplekst tall
Algebraiske og trigonometriske former for et komplekst tall
Eksponentiell form av et komplekst tall
Euler formler
§ 2. Hele funksjoner (polynomer) og deres grunnleggende egenskaper. Løsning av algebraiske ligninger på settet med komplekse tall
Definisjon av en algebraisk ligning av th grad
Grunnleggende egenskaper ved polynomer
Eksempler på løsning av algebraiske ligninger på settet med komplekse tall
Spørsmål til selvransakelse
Ordliste
§ 1. Komplekse tall: definisjoner, geometrisk tolkning, operasjoner i algebraiske, trigonometriske og eksponentielle former
Definisjon av et komplekst tall ( Formuler definisjonen av et komplekst tall)
Et komplekst tall z er et uttrykk av følgende form:
Kompleks tall i algebraisk form,(1)
hvor x, y Î;
- komplekst konjugat nummer z ;
- motsatt tall nummer z ;
- kompleks null ;
- dette er settet med komplekse tall.
1)z = 1 + JegÞ Re z= 1, Im z = 1, = 1 – Jeg, = –1 – Jeg ;
2)z = –1 + JegÞ Re z= –1, Im z = , = –1 – Jeg, = –1 –Jeg ;
3)z = 5 + 0Jeg= 5 Þ Re z= 5, Im z = 0, = 5 – 0Jeg = 5, = –5 – 0Jeg = –5
Þ hvis jeg z= 0, da z = x- ekte nummer;
4)z = 0 + 3Jeg = 3JegÞ Re z= 0, Im z = 3, = 0 – 3Jeg = –3Jeg , = –0 – 3Jeg = – 3Jeg
Þ hvis Re z= 0, da z = iy - rent imaginært tall.
Komplekse likheter (Formuler betydningen av kompleks likhet)
1)  ;
;
2) .
.
En kompleks likhet tilsvarer et system med to reelle likheter. Disse reelle likhetene oppnås fra den komplekse likheten ved å skille de reelle og imaginære delene.
1) ![]() ;
;
2) ![]() .
.
Geometrisk representasjon av komplekse tall ( Hva er den geometriske representasjonen av komplekse tall?)

Komplekst tall z representert med en prikk ( x , y) på det komplekse planet eller radiusvektoren til dette punktet.
Skilt z i andre kvadrant betyr at det kartesiske koordinatsystemet vil bli brukt som det komplekse planet.
Modul og argument for et komplekst tall ( Hva er modulen og argumentet til et komplekst tall?)
Modulen til et komplekst tall er et ikke-negativt reelt tall
![]() .(2)
.(2)
Geometrisk er modulen til et komplekst tall lengden på vektoren som representerer tallet z, eller polarradiusen til et punkt ( x , y).
Tegn følgende tall på det komplekse planet og skriv dem i trigonometrisk form.
1)z = 1 + Jeg Þ
![]() ,
,
Þ ![]()
Þ ![]() ;
;

![]() ,
,
Þ ![]()
Þ ![]() ;
;

![]() ,
,


5)![]() ,
,

det vil si at for z = 0 vil det være
, j ikke bestemt.
Aritmetiske operasjoner på komplekse tall (Gi definisjoner og liste opp hovedegenskapene til aritmetiske operasjoner på komplekse tall.)
Addisjon (subtraksjon) av komplekse tall
z 1 ± z 2 = (x 1 + iy 1)±( x 2 + iy 2) = (x 1 ± x 2) + Jeg (y 1 ± y 2),(5)
det vil si at når man legger til (subtraherer) komplekse tall, blir deres reelle og imaginære deler lagt til (trukket fra).
1)(1 + Jeg) + (2 – 3Jeg) = 1 + Jeg + 2 –3Jeg = 3 – 2Jeg ;
2)(1 + 2Jeg) – (2 – 5Jeg) = 1 + 2Jeg – 2 + 5Jeg = –1 + 7Jeg .
Grunnleggende egenskaper ved tilsetning
1)z 1 + z 2 = z 2 + z 1;
2)z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3);
3)z 1 – z 2 = z 1 + (– z 2);
4)z + (–z) = 0;
Multiplikasjon av komplekse tall i algebraisk form
z 1∙z 2 = (x 1 + iy 1)∙(x 2 + iy 2) = x 1x 2 + x 1iy 2 + iy 1x 2 + Jeg 2y 1y 2 = (6)
= (x 1x 2 – y 1y 2) + Jeg (x 1y 2 + y 1x 2),
det vil si at multiplikasjonen av komplekse tall i algebraisk form utføres i henhold til regelen om algebraisk multiplikasjon av et binomial med et binomial, etterfulgt av erstatning og reduksjon av lignende i reelle og imaginære termer.
1)(1 + Jeg)∙(2 – 3Jeg) = 2 – 3Jeg + 2Jeg – 3Jeg 2 = 2 – 3Jeg + 2Jeg + 3 = 5 – Jeg ;
2)(1 + 4Jeg)∙(1 – 4Jeg) = 1 – 42 Jeg 2 = 1 + 16 = 17;
3)(2 + Jeg)2 = 22 + 4Jeg + Jeg 2 = 3 + 4Jeg .
Multiplikasjon av komplekse tall trigonometrisk form
z 1∙z 2 = r 1 (cos j 1 + Jeg synd j 1)× r 2 (cos j 2 + Jeg synd j 2) =
= r 1r 2 (cos j 1cos j 2 + Jeg cos j 1sin j 2 + Jeg synd j 1cos j 2 + Jeg 2 synd j 1sin j 2) =
= r 1r 2((cos j 1cos j 2-synd j 1sin j 2) + Jeg(cos j 1sin j 2+ synd j 1cos j 2))
Produktet av komplekse tall i trigonometrisk form, det vil si at når komplekse tall multipliseres i trigonometrisk form, multipliseres modulene deres og argumentene legges til.

Grunnleggende egenskaper ved multiplikasjon
1)z 1× z 2 = z 2× z 1 - kommutativitet;
2)z 1× z 2× z 3 = (z 1× z 2)× z 3 = z 1×( z 2× z 3) - assosiativitet;
3)z 1×( z 2 + z 3) = z 1× z 2 + z 1× z 3 - distributivitet med hensyn til tillegg;
4)z×0 = 0; z×1 = z ;
Divisjon av komplekse tall
Divisjon er det inverse av multiplikasjon, altså
hvis z × z 2 = z 1 og z 2¹ 0, deretter .
Når du utfører divisjon i algebraisk form, multipliseres telleren og nevneren til brøken med det komplekse konjugatet til nevneren:
 Divisjon av komplekse tall i algebraisk form.(7)
Divisjon av komplekse tall i algebraisk form.(7)
Når du utfører divisjon i trigonometrisk form, deles moduler og argumenter trekkes fra:
 Divisjon av komplekse tall i trigonometrisk form.(8)
Divisjon av komplekse tall i trigonometrisk form.(8)
2) .
.
Heve et komplekst tall til en naturlig potens
Å heve til en naturlig kraft er mer praktisk å utføre i trigonometrisk form:
![]()
Moivre formel,(9)
det vil si at når et komplekst tall heves til en naturlig potens, heves dets modul til den potensen, og argumentet multipliseres med eksponenten.
Beregn (1 + Jeg)10.

Merknader
1. Når du utfører operasjoner med multiplikasjon og heving til en naturlig potens i trigonometrisk form, kan vinkelverdier oppnås utenfor en hel omdreining. Men de kan alltid reduseres til vinkler eller ved å slippe et helt antall komplette omdreininger i henhold til periodisitetsegenskapene til funksjonene og .
2. Mening ![]() kalles hovedverdien til argumentet til et komplekst tall;
kalles hovedverdien til argumentet til et komplekst tall;
i dette tilfellet angir verdiene for alle mulige vinkler ;
det er åpenbart at .
Trekke ut roten til en naturlig grad fra et komplekst tall
 Euler-formler(16)
Euler-formler(16)
der trigonometriske funksjoner og en reell variabel uttrykkes i form av en eksponentiell funksjon (eksponent) med en rent imaginær eksponent.
§ 2. Hele funksjoner (polynomer) og deres grunnleggende egenskaper. Løsning av algebraiske ligninger på settet med komplekse tall
To polynomer av samme grad n er identisk like med hverandre hvis og bare hvis koeffisientene deres sammenfaller med samme potenser av variabelen x, det er
Bevis
w Identitet (3) gjelder for "xн (eller "xн)
Þ den er gyldig for ; erstatter, får vi an = mrd .
La oss gjensidig utslette vilkårene i (3) an og mrd og dele begge deler med x :
Denne identiteten gjelder også for " x, inkludert når x = 0
Þ forutsatt x= 0, får vi an – 1 = mrd – 1.
Gjensidig utslette i (3") termer an– 1 og en n– 1 og del begge deler med x, som et resultat får vi
Fortsetter vi argumentet på samme måte, får vi det an – 2 = mrd –2, …, en 0 = b 0.
Dermed er det bevist at fra den identiske likheten til 2-x polynomer følger sammenfallet av koeffisientene deres i samme grader x .
Det omvendte utsagnet er med rette åpenbart, dvs. hvis to polynomer har de samme alle koeffisientene, så er de de samme funksjonene, derfor er verdiene deres de samme for alle verdiene av argumentet, noe som betyr at de er identiske. Eiendom 1 er påvist fullstendig. v
Når du deler et polynom PN (x) til forskjellen ( x – X 0) resten er lik PN (x 0), altså
![]() Bezouts teorem, (4)
Bezouts teorem, (4)
hvor Qn – 1(x) - heltallsdelen av divisjon, er et polynom av grad ( n – 1).
Bevis
w La oss skrive divisjonsformelen med en rest:
PN (x) = (x – X 0)∙Qn – 1(x) + EN ,
hvor Qn – 1(x) - gradspolynom ( n – 1),
EN- resten, som er et tall på grunn av den velkjente algoritmen for å dele et polynom i et binomium "i en kolonne".
Denne likheten gjelder for " x, inkludert når x = X 0 Þ
PN (x 0) = (x 0 – x 0)× Qn – 1(x 0) + EN Þ
EN = PN (X 0), h.t.d. v
Konsekvens fra Bezouts teorem. På deling av et polynom med et binomium uten en rest
Hvis nummer X 0 er null av polynomet, så er dette polynomet delelig med forskjellen ( x – X 0) uten rest, altså
Þ ![]() .(5)
.(5)
1), fordi P 3(1) º 0
2) , fordi P 4(–2) º 0
3) fordi P 2(–1/2) º 0
Inndeling av polynomer i binomer "i en kolonne":
| _ | _ | |||||||||||||
| _ | _ | |||||||||||||
| _ | ||||||||||||||
Hvert polynom med grad n ³ 1 har minst en null, reell eller kompleks
Beviset for denne teoremet ligger utenfor rammen av kurset vårt. Derfor aksepterer vi teoremet uten bevis.
La oss jobbe med denne teoremet og Bezouts teorem med et polynom PN (x).
Etter n-fold anvendelse av disse teoremene, får vi det
hvor en 0 er koeffisienten ved x n i PN (x).
Konsekvens fra algebras grunnleggende teorem. Om dekomponering av et polynom til lineære faktorer
Ethvert polynom av grad på settet med komplekse tall dekomponeres til n lineære faktorer, altså
Dekomponering av et polynom i lineære faktorer, (6)
hvor x1, x2, ... xn er nullpunktene til polynomet.
Samtidig, hvis k tall fra settet X 1, X 2, … xn faller sammen med hverandre og med tallet a, så i produktet (6) faktoren ( x– a) k. Så nummeret x= a kalles k-fold null polynom PN ( x) . Hvis en k= 1, så kalles null enkelt nullpolynom PN ( x) .
1)P 4(x) = (x – 2)(x– 4)3 Þ x 1 = 2 - enkel null, x 2 = 4 - trippel null;
2)P 4(x) = (x – Jeg)4 x = Jeg- null multiplisitet 4.
Egenskap 4 (på antall røtter til en algebraisk ligning)
Enhver algebraisk ligning Pn(x) = 0 av grad n har nøyaktig n røtter på settet med komplekse tall hvis hver rot telles like mange ganger som dens multiplisitet.
1)x 2 – 4x+ 5 = 0 - algebraisk ligning av andre grad
Þ x 1,2 = 2 ± = 2 ± Jeg- to røtter;
2)x 3 + 1 = 0 - algebraisk likning av tredje grad
Þ x
1,2,3 =  - tre røtter;
- tre røtter;
3)P 3(x) = x 3 + x 2 – x– 1 = 0 x 1 = 1, fordi P 3(1) = 0.
Del polynomet P 3(x) på ( x – 1):
| x 3 | + | x 2 | – | x | – | 1 | x – 1 |
| x 3 | – | x 2 | x 2 + 2x +1 | ||||
| 2x 2 | – | x | |||||
| 2x 2 | – | 2x | |||||
| x | – | 1 | |||||
| x | – | 1 | |||||
| 0 |
Innledende ligning
P 3(x) = x 3 + x 2 – x– 1 = 0 Û( x – 1)(x 2 + 2x+ 1) = 0 w( x – 1)(x + 1)2 = 0
Þ x 1 = 1 - enkel rot, x 2 \u003d -1 - dobbel rot.
1) er sammenkoblede komplekse konjugerte røtter;
Ethvert polynom med reelle koeffisienter dekomponeres til et produkt av lineære og kvadratiske funksjoner med reelle koeffisienter.
Bevis
w La x 0 = en + bi- polynom null PN (x). Hvis alle koeffisientene til dette polynomet er reelle tall, er det også null (ved egenskap 5).
Vi beregner produktet av binomialer ![]() :
:
kompleks tall polynom ligning
Fikk ( x – en)2 + b 2 - kvadrattrinomial med reelle koeffisienter.
Dermed fører ethvert par binomialer med komplekse konjugerte røtter i formel (6) til et kvadratisk trinomium med reelle koeffisienter. v
1)P 3(x) = x 3 + 1 = (x + 1)(x 2 – x + 1);
2)P 4(x) = x 4 – x 3 + 4x 2 – 4x = x (x –1)(x 2 + 4).
Eksempler på å løse algebraiske ligninger på settet med komplekse tall ( Gi eksempler på løsning av algebraiske ligninger på settet med komplekse tall)
1. Algebraiske ligninger av første grad:
, er den eneste enkle roten.
2. Kvadratiske ligninger:
![]() ,
, ![]() - har alltid to røtter (ulike eller like).
- har alltid to røtter (ulike eller like).
1) ![]() .
.
3. To-term gradsligninger:
,- har alltid forskjellige røtter.
![]() ,
,
Svar: , ![]() .
.
4. Løs kubikkligningen.
En likning av tredje grad har tre røtter (reelle eller kompleks), og hver rot må telles like mange ganger som dens multiplisitet. Siden alle koeffisientene til denne ligningen er reelle tall, vil de komplekse røttene til ligningen, hvis noen, være sammenkoblet kompleks konjugert.
Ved seleksjon finner vi den første roten av ligningen, siden .
Av en følge av Bezouts teorem. Vi beregner denne divisjonen "i en kolonne":
| _ | |||||
| _ | |||||
| _ | |||||
Ved å representere polynomet som et produkt av en lineær og kvadratisk faktor, får vi:
![]() .
.
Vi finner andre røtter som røttene til den kvadratiske ligningen: ![]()
Svar: , ![]() .
.
5. Lag en algebraisk ligning av minste grad med reelle koeffisienter, hvis det er kjent at tallene x 1 = 3 og x 2 = 1 + Jeg er dens røtter, og x 1 er en dobbeltrot, og x 2 - enkelt.
Tallet er også roten til ligningen, fordi koeffisientene til ligningen må være reelle.
Totalt har den ønskede ligningen 4 røtter: x 1, x 1,x 2,. Derfor er graden 4. Vi komponerer et polynom av 4. grad med nuller x
11. Hva er kompleks null?
13. Formuler betydningen av kompleks likhet.
15. Hva er modulen og argumentet til et komplekst tall?
17. Hva er argumentet til et komplekst tall?
18. Hva er navnet eller betydningen av formelen?
19. Forklar betydningen av notasjonen i denne formelen:
27. Gi definisjoner og liste opp hovedegenskapene til aritmetiske operasjoner på komplekse tall.
28. Hva er navnet eller betydningen av formelen?
29. Forklar betydningen av notasjonen i denne formelen:
31. Hva er navnet eller betydningen av formelen?
32. Forklar betydningen av notasjonen i denne formelen:
34. Hva er navnet eller betydningen av formelen?
35. Forklar betydningen av notasjonen i denne formelen:
61. Liste hovedegenskapene til polynomer.
63. Formuler en egenskap om å dele et polynom med en forskjell (x - x0).
65. Hva er navnet eller betydningen av formelen?
66. Forklar betydningen av notasjonen i denne formelen:
67. ⌂ ![]() .
.
69. Formuler teoremet algebraens teorem er grunnleggende.
70. Hva er navnet eller betydningen av formelen?
71. Forklar betydningen av notasjonen i denne formelen:
75. Formuler en egenskap om antall røtter til en algebraisk ligning.
78. Formuler en egenskap om dekomponering av et polynom med reelle koeffisienter til lineære og kvadratiske faktorer.
Ordliste
K-fold null i et polynom kalles... (s. 18)
et algebraisk polynom kalles... (s. 14)
en algebraisk ligning av n. grad kalles ... (s. 14)
den algebraiske formen til et komplekst tall kalles... (s. 5)
argumentet til et komplekst tall er... (s. 4)
den reelle delen av det komplekse tallet z er... (side 2)
det komplekse konjugatet er... (side 2)
kompleks null er... (side 2)
et komplekst tall kalles... (s. 2)
den n-te roten av et komplekst tall kalles... (s. 10)
roten til ligningen kalles ... (s. 14)
polynomkoeffisienter er... (s. 14)
den imaginære enheten er... (side 2)
den imaginære delen av et komplekst tall z er... (side 2)
modulen til et komplekst tall kalles... (s. 4)
nullpunktet til en funksjon kalles... (s. 14)
eksponentiell form av et komplekst tall kalles... (s. 11)
et polynom kalles... (s. 14)
den enkle nullen til et polynom kalles... (s. 18)
det motsatte tallet er... (side 2)
graden av et polynom er... (s. 14)
den trigonometriske formen til et komplekst tall kalles... (s. 5)
De Moivres formel er... (s. 9)
Eulers formler er... (s. 13)
en hel funksjon kalles... (s. 14)
et rent imaginært tall er... (s. 2)
Bruke kalkulatoren
For å evaluere et uttrykk, må du skrive inn en streng for å evaluere. Når du legger inn tall, er desimalskilletegnet et punktum. Parentes kan brukes. Operasjoner på komplekse tall er multiplikasjon (*), divisjon (/), addisjon (+), subtraksjon (-), eksponentiering (^) og andre. Som en registrering av komplekse tall kan du bruke eksponentiell og algebraisk form. Skriv inn en tenkt enhet Jeg mulig uten multiplikasjonstegn, i andre tilfeller kreves multiplikasjonstegnet, for eksempel mellom parentes eller mellom et tall og en konstant. Konstanter kan også brukes: tallet π legges inn som pi, eksponenten e, må alle uttrykk i eksponenten omsluttes i parentes.
Eksempelstreng å beregne: (4,5+i12)*(3,2i-2,5)/e^(i1,25*pi), som tilsvarer uttrykket \[\frac((4(,)5 + i12)(3(,)2i-2(,)5))(e^(i1(,)25\pi))\]
Kalkulatoren kan bruke konstanter, matematiske funksjoner, tilleggsoperasjoner og mer komplekse uttrykk, du kan gjøre deg kjent med disse funksjonene på siden med generelle regler for bruk av kalkulatorer på dette nettstedet.
Siden er under konstruksjon, noen sider er kanskje ikke tilgjengelige.
Nyheter
07.07.2016
Lagt til en kalkulator for å løse systemer med ikke-lineære algebraiske ligninger: .
30.06.2016
Siden har et responsivt design, sidene vises tilstrekkelig både på store skjermer og på mobile enheter.
Sponsor
RGOnline.ru - en umiddelbar løsning for elektrisk arbeid på nettet.
Hva annet å lese
DE SISTE NOTER
- "The Tale of Bygone Years" - et enestående monument av gammel russisk litteratur
- Pushkin "Jeg husker et fantastisk øyeblikk": analyse av diktet
- Ferie. Gjennomgang av R. Bradburys historie "Holidays" Rugby helligdager hovedpersoner og sammendrag
- Hva advarer fonvizin om komedie underskog
- Esoteriske symboler og tegn Gode symboler
