Ketaksamaan trigonometri berganda. Algoritma untuk menyelesaikan ketaksamaan trigonometri yang paling mudah dan mengenali cara untuk menyelesaikan ketaksamaan trigonometri.
Kebanyakan pelajar tidak menyukai ketaksamaan trigonometri. Tetapi sia-sia. Seperti yang pernah dikatakan oleh seorang watak,
“Anda tidak tahu cara memasaknya”
Jadi bagaimana untuk "memasak" dan dengan apa untuk menyerahkan ketidaksamaan dengan sinus, kami akan memikirkannya dalam artikel ini. Kami akan membuat keputusan dengan cara yang mudah menggunakan bulatan unit.
Jadi, pertama sekali, kita perlukan algoritma berikut.
Algoritma untuk menyelesaikan ketaksamaan dengan sinus:
- letakkan nombor $a$ pada paksi sinus dan lukis garis lurus selari dengan paksi kosinus sehingga ia bersilang dengan bulatan;
- titik persilangan garis ini dengan bulatan akan diisi jika ketaksamaan tidak ketat, dan tidak diisi jika ketaksamaan adalah ketat;
- kawasan penyelesaian ketaksamaan akan berada di atas garisan dan sehingga bulatan jika ketaksamaan mengandungi tanda “$>$”, dan di bawah garisan dan sehingga bulatan jika ketaksamaan mengandungi tanda “$<$”;
- untuk mencari titik persilangan, kita selesaikan persamaan trigonometri $\sin(x)=a$, kita dapat $x=(-1)^(n)\arcsin(a) + \pi n$;
- menetapkan $n=0$, kita dapati titik persilangan pertama (ia terletak sama ada di kuadran pertama atau keempat);
- untuk mencari titik kedua, kita melihat ke arah mana kita akan melintasi kawasan itu ke titik persimpangan kedua: jika dalam arah positif, maka $n=1$ harus diambil, dan jika dalam arah negatif, maka $n= -1$;
- sebagai tindak balas, selang dari titik persilangan yang lebih kecil $+ 2\pi n$ kepada yang lebih besar $+ 2\pi n$ ditulis.
Had algoritma
Penting: d algoritma ini tidak berfungsi untuk ketaksamaan dalam bentuk $\sin(x) > 1; \ \sin(x) \geq 1, \ \sin(x)< -1, \ \sin{x} \leq -1$. В строгом случае эти неравенства не имеют решений, а в нестрогом – решение сводится к решению уравнения $\sin{x} = 1$ или $\sin{x} = -1$.
Kes khas apabila menyelesaikan ketaksamaan dengan sinus
Ia juga penting untuk diperhatikan kes berikut, yang lebih mudah untuk diselesaikan secara logik tanpa menggunakan algoritma di atas.
kes istimewa 1. Selesaikan ketaksamaan:
$\sin(x) \leq 1.$
Oleh kerana domain fungsi trigonometri $y=\sin(x)$ ialah paling banyak $1$, bahagian kiri ketaksamaan bagi apa apa$x$ daripada domain (dan domain sinus adalah semua nombor nyata) paling banyak $1$. Dan, oleh itu, sebagai tindak balas kami menulis: $x \dalam R$.
Akibat:
$\sin(x) \geq -1.$
Kes khas 2. Selesaikan ketaksamaan:
$\sin(x)< 1.$
Menggunakan hujah yang serupa dengan kes khas 1, kita dapati bahawa bahagian kiri ketaksamaan adalah kurang daripada $1$ untuk semua $x \dalam R$, kecuali untuk titik-titik yang merupakan penyelesaian persamaan $\sin(x) = 1 $. Menyelesaikan persamaan ini, kita akan mempunyai:
$x = (-1)^(n)\arcsin(1)+ \pi n = (-1)^(n)\frac(\pi)(2) + \pi n.$
Dan, oleh itu, sebagai tindak balas kami menulis: $x \in R \backslash \left\((-1)^(n)\frac(\pi)(2) + \pi n\right\)$.
Akibat: ketidaksamaan diselesaikan dengan cara yang sama
$\sin(x) > -1.$
Contoh penyelesaian ketaksamaan menggunakan algoritma.
Contoh 1: Selesaikan ketaksamaan:
$\sin(x) \geq \frac(1)(2).$
- Perhatikan koordinat $\frac(1)(2)$ pada paksi sinus.
- Lukis garis selari dengan paksi kosinus dan melalui titik ini.
- Perhatikan titik persimpangan. Mereka akan teduh kerana ketidaksamaan itu tidak ketat.
- Tanda ketidaksamaan ialah $\geq$, yang bermaksud bahawa kami melukis di atas kawasan di atas garisan, i.e. separuh bulatan yang lebih kecil.
- Cari titik persilangan pertama. Untuk melakukan ini, tukar ketaksamaan kepada kesamaan dan selesaikannya: $\sin(x)=\frac(1)(2) \ \Rightarrow \ x=(-1)^(n)\arcsin(\frac(1 )(2) )+\pi n =(-1)^(n)\frac(\pi)(6) + \pi n$. Kami selanjutnya menetapkan $n=0$ dan mencari titik persilangan pertama: $x_(1)=\frac(\pi)(6)$.
- Kami mencari titik kedua. Kawasan kami menuju ke arah positif dari titik pertama, jadi kami menetapkan $n$ sama dengan $1$: $x_(2)=(-1)^(1)\frac(\pi)(6) + \pi \ cdot 1 = \ pi - \frac(\pi)(6) = \frac(5\pi)(6)$.
Oleh itu, penyelesaiannya akan mengambil bentuk:
$x \dalam \kiri[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\kanan], \ n \dalam Z.$
Contoh 2: Selesaikan ketaksamaan:
$\sin(x)< -\frac{1}{2}$
Kami menandakan koordinat $- \frac(1)(2)$ pada paksi sinus dan lukis garis lurus selari dengan paksi kosinus dan melalui titik ini. Perhatikan titik persimpangan. Mereka tidak akan teduh, kerana ketidaksamaan adalah ketat. Tanda ketidaksamaan $<$, а, значит, закрашиваем область ниже прямой, т.е. меньший полукруг. Неравенство превращаем в равенство и решаем его:
$\sin(x)=-\frac(1)(2)$
$x=(-1)^(n)\arcsin(\kiri(-\frac(1)(2)\kanan))+ \pi n =(-1)^(n+1)\frac(\pi )(6) + \pi n$.
Menetapkan lebih jauh $n=0$, kita dapati titik persilangan pertama: $x_(1)=-\frac(\pi)(6)$. Kawasan kami pergi ke arah negatif dari titik pertama, jadi kami menetapkan $n$ sama dengan $-1$: $x_(2)=(-1)^(-1+1)\frac(\pi)(6 ) + \pi \cdot (-1) = -\pi + \frac(\pi)(6) = -\frac(5\pi)(6)$.
Jadi, penyelesaian kepada ketidaksamaan ini ialah selang:
$x \dalam \kiri(-\frac(5\pi)(6) + 2\pi n; -\frac(\pi)(6) + 2 \pi n\kanan), \ n \dalam Z.$
Contoh 3: Selesaikan ketaksamaan:
$1 – 2\sin(\kiri(\frac(x)(4)+\frac(\pi)(6)\kanan)) \leq 0.$
Contoh ini tidak boleh diselesaikan dengan segera menggunakan algoritma. Mula-mula anda perlu menukarnya. Kami melakukan persis seperti yang akan kami lakukan dengan persamaan, tetapi jangan lupa tentang tanda itu. Membahagi atau mendarab dengan nombor negatif membalikkannya!
Jadi, mari kita alihkan semua yang tidak mengandungi fungsi trigonometri ke sebelah kanan. Kita mendapatkan:
$- 2\sin(\kiri(\frac(x)(4)+\frac(\pi)(6)\kanan)) \leq -1.$
Bahagikan bahagian kiri dan kanan dengan $-2$ (jangan lupa tentang tanda!). Pasti akan:
$\sin(\left(\frac(x)(4)+\frac(\pi)(6)\kanan)) \geq \frac(1)(2).$
Sekali lagi, kami mendapat ketidaksamaan yang tidak dapat kami selesaikan menggunakan algoritma. Tetapi di sini sudah cukup untuk membuat perubahan pembolehubah:
$t=\frac(x)(4)+\frac(\pi)(6).$
Kami mendapat ketaksamaan trigonometri, yang boleh diselesaikan menggunakan algoritma:
$\sin(t) \geq \frac(1)(2).$
Ketaksamaan ini telah diselesaikan dalam contoh 1, jadi kami akan meminjam jawapan dari sana:
$t \in \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\kanan].$
Namun, keputusan itu masih belum berakhir. Kita perlu kembali kepada pembolehubah asal.
$(\frac(x)(4)+\frac(\pi)(6)) \dalam \left[\frac(\pi)(6) + 2\pi n; \frac(5\pi)(6) + 2 \pi n\kanan].$
Mari kita wakili jurang sebagai sistem:
$\left\(\begin(array)(c) \frac(x)(4)+\frac(\pi)(6) \geq \frac(\pi)(6) + 2\pi n, \\ \frac(x)(4)+\frac(\pi)(6) \leq \frac(5\pi)(6) + 2 \pi n.\end(array) \kanan.$
Di sebelah kiri sistem ialah ungkapan ($\frac(x)(4)+\frac(\pi)(6)$), yang tergolong dalam selang. Sempadan kiri selang bertanggungjawab untuk ketaksamaan pertama, dan sempadan kanan bertanggungjawab untuk yang kedua. Selain itu, kurungan memainkan peranan penting: jika kurungan adalah persegi, maka ketidaksamaan akan menjadi tidak ketat, dan jika ia bulat, maka ketat. tugas kita ialah mendapatkan $x$ di sebelah kiri dalam kedua-dua ketidaksamaan.
Mari kita alihkan $\frac(\pi)(6)$ dari sebelah kiri ke sebelah kanan, kita dapat:
$\left\(\begin(array)(c) \frac(x)(4) \geq \frac(\pi)(6) + 2\pi n -\frac(\pi)(6), \\ \frac(x)(4) \leq \frac(5\pi)(6) + 2 \pi n – \frac(\pi)(6).\end(array) \kanan.$
Memudahkan, kita akan mempunyai:
$\left\(\begin(array)(c) \frac(x)(4) \geq 2\pi n, \\ \frac(x)(4) \leq \frac(2\pi)(3) + 2 \pi n.\end(array) \right.$
Mendarabkan sisi kiri dan kanan dengan $4$, kita dapat:
$\left\(\begin(array)(c) x \geq 8\pi n, \\ x \leq \frac(8\pi)(3) + 8 \pi n. \end(array) \right. $
Memasang sistem ke dalam selang, kami mendapat jawapannya:
$x \dalam \kiri[ 8\pi n; \frac(8\pi)(3) + 8 \pi n\kanan], \ n \dalam Z.$
Projek algebra "Penyelesaian ketaksamaan trigonometri" Disiapkan oleh pelajar kelas 10 "B" Julia Kazachkova Penyelia: guru matematik Kochakova N.N.
Tujuan Untuk menyatukan bahan mengenai topik "Menyelesaikan ketaksamaan trigonometri" dan mencipta memo untuk pelajar bersedia untuk peperiksaan yang akan datang.
Objektif Merumuskan bahan mengenai topik. Susun maklumat yang diterima. Pertimbangkan topik ini dalam peperiksaan.
Perkaitan Kaitan topik yang saya pilih terletak pada fakta bahawa tugasan mengenai topik "Penyelesaian ketaksamaan trigonometri" dimasukkan ke dalam tugasan peperiksaan.
Ketaksamaan trigonometri Ketaksamaan ialah hubungan yang menghubungkan dua nombor atau ungkapan melalui salah satu tanda: (lebih besar daripada); ≥ (lebih besar daripada atau sama dengan). Ketaksamaan trigonometri ialah ketaksamaan yang mengandungi fungsi trigonometri.
Ketaksamaan trigonometri Penyelesaian ketaksamaan yang mengandungi fungsi trigonometri dikurangkan, sebagai peraturan, kepada penyelesaian ketaksamaan termudah dalam bentuk: sin x>a, sin x a, cos x a, tgx a, ctg x
Algoritma untuk menyelesaikan ketaksamaan trigonometri Pada paksi yang sepadan dengan fungsi trigonometri yang diberikan, tandakan nilai berangka yang diberikan bagi fungsi ini. Lukis garisan melalui titik bertanda yang bersilang dengan bulatan unit. Pilih titik persilangan garis dan bulatan, dengan mengambil kira tanda ketidaksamaan yang ketat atau tidak ketat. Pilih lengkok bulatan di mana penyelesaian ketaksamaan terletak. Tentukan nilai sudut pada titik permulaan dan akhir lengkok bulat. Tuliskan penyelesaian ketaksamaan, dengan mengambil kira keberkalaan fungsi trigonometri yang diberikan.
Formula untuk menyelesaikan ketaksamaan trigonometri sinx >a; x (arcsin a + 2πn; π- arcsin a + 2πn). sinx a; x (- arccos a + 2πn; arccos a + 2πn). cosxa; x (arctg a + πn ; + πn). tgx a; x (πn ; arctg + πn). ctgx
Penyelesaian grafik ketaksamaan trigonometri asas sinx >a
Penyelesaian grafik bagi ketaksamaan trigonometri utama sinx Penyelesaian grafik bagi ketaksamaan trigonometri utama cosx >a Penyelesaian grafik bagi ketaksamaan trigonometri utama cosx Penyelesaian grafik bagi ketaksamaan trigonometri utama tgx >a Penyelesaian grafik bagi ketaksamaan trigonometri utama tgx Penyelesaian grafik bagi ketaksamaan trigonometri utama ctgx >a
1. Jika hujahnya rumit (berbeza dengan X), kemudian kami menggantikannya dengan t.
2. Kami membina dalam satu satah koordinat mainan graf fungsi y=kos dan y=a.
3. Kami dapati sedemikian dua titik persilangan graf yang bersebelahan, antara yang terletak di atas garis y=a. Cari absis bagi mata ini.
4. Tulis ketaksamaan berganda untuk hujah t, dengan mengambil kira tempoh kosinus ( t akan berada di antara abscissas yang ditemui).
5. Lakukan penggantian terbalik (kembali kepada hujah asal) dan nyatakan nilainya X daripada ketaksamaan berganda, kami menulis jawapan sebagai selang berangka.
Contoh 1
Selanjutnya, mengikut algoritma, kami menentukan nilai hujah tersebut t, di mana sinusoid berada di atas lurus. Kami menulis nilai ini sebagai ketaksamaan berganda, dengan mengambil kira keberkalaan fungsi kosinus, dan kemudian kembali kepada hujah asal X.
Contoh 2
Memilih julat nilai t yang mana sinusoid berada di atas garis lurus.
Kami menulis dalam bentuk ketaksamaan berganda nilai t, memenuhi syarat. Jangan lupa bahawa tempoh terkecil fungsi y=kos sama 2π. Kembali ke Pembolehubah X, secara beransur-ansur memudahkan semua bahagian ketaksamaan berganda.
Kami menulis jawapan sebagai selang berangka tertutup, kerana ketidaksamaan itu tidak ketat.
Contoh 3
Kami akan berminat dengan julat nilai t, di mana titik sinusoid akan terletak di atas garis lurus.
Nilai t kita menulis dalam bentuk ketaksamaan berganda, kita menulis semula nilai yang sama untuk 2x dan menyatakan X. Kami menulis jawapan sebagai selang berangka.
Dan lagi formula kos>a.
Sekiranya kos>a, (-1≤a≤1), kemudian - arccos a + 2πn< t < arccos a + 2πn, nєZ.
Gunakan formula untuk menyelesaikan ketaksamaan trigonometri dan menjimatkan masa pada ujian peperiksaan.
Dan sekarang formula
, yang harus anda gunakan pada peperiksaan UNT atau USE apabila menyelesaikan ketaksamaan trigonometri dalam bentuk kos
Sekiranya kos , (-1≤a≤1), kemudian arccos a + 2πn< t < 2π — arccos a + 2πn, nєZ.
Gunakan formula ini untuk menyelesaikan ketaksamaan yang dibincangkan dalam artikel ini, dan anda akan mendapat jawapan dengan lebih pantas dan tanpa sebarang graf!
Dengan mengambil kira keberkalaan fungsi sinus, kami menulis ketidaksamaan berganda untuk nilai hujah t, yang memenuhi ketidaksamaan terakhir. Mari kita kembali kepada pembolehubah asal. Mari kita ubah ketaksamaan berganda yang terhasil dan nyatakan pembolehubah X. Kami menulis jawapan sebagai selang.
Kami menyelesaikan ketidaksamaan kedua:
Apabila menyelesaikan ketaksamaan kedua, kita perlu mengubah bahagian kiri ketaksamaan ini menggunakan formula sinus hujah berganda untuk mendapatkan ketaksamaan bentuk: sint≥a. Seterusnya, kami mengikuti algoritma.
Kami menyelesaikan ketidaksamaan ketiga:
Graduan dan pemohon yang dihormati! Perlu diingat bahawa kaedah sedemikian untuk menyelesaikan ketaksamaan trigonometri, seperti kaedah grafik di atas dan, pastinya, anda tahu, kaedah penyelesaian menggunakan bulatan trigonometri unit (bulatan trigonometri) hanya terpakai pada peringkat pertama mempelajari bahagian trigonometri. "Penyelesaian persamaan trigonometri dan ketaksamaan". Saya fikir anda akan ingat bahawa anda mula-mula menyelesaikan persamaan trigonometri yang paling mudah menggunakan graf atau bulatan. Walau bagaimanapun, kini anda tidak terfikir untuk menyelesaikan persamaan trigonometri dengan cara ini. Bagaimana anda menyelesaikannya? Betul, formula. Jadi ketaksamaan trigonometri harus diselesaikan dengan formula, terutamanya semasa ujian, apabila jalan setiap minit. Jadi, selesaikan tiga ketaksamaan pelajaran ini menggunakan rumus yang sesuai.
Sekiranya sint>a, di mana -1≤ a≤1, maka arcsin a + 2πn< t < π — arcsin a + 2πn, nºZ.
Belajar formula!
Dan akhirnya: adakah anda tahu bahawa matematik adalah definisi, peraturan dan FORMULA?!
Sudah tentu anda lakukan! Dan yang paling ingin tahu, setelah mempelajari artikel ini dan menonton video itu, berseru: "Betapa lama dan sukar! Adakah terdapat formula yang membolehkan anda menyelesaikan ketaksamaan tersebut tanpa sebarang graf dan bulatan? Ya, sudah tentu ada!
UNTUK MENYELESAIKAN KETIDAKSAMAAN PANDANGAN: sint (-1≤a≤1) formula adalah sah:
- π - lengkok a + 2πn< t < arcsin a + 2πn, nєZ.
Gunakannya pada contoh yang dipertimbangkan dan anda akan mendapat jawapan dengan lebih cepat!
Kesimpulan: BELAJAR FORMULA, KAWAN!
Muka surat 1 daripada 1 1
1.5 Ketaksamaan trigonometri dan kaedah penyelesaiannya
1.5.1 Menyelesaikan ketaksamaan trigonometri mudah
Kebanyakan pengarang buku teks moden mengenai matematik mencadangkan agar kita memulakan pertimbangan kita tentang topik ini dengan menyelesaikan ketaksamaan trigonometri yang paling mudah. Prinsip menyelesaikan ketaksamaan trigonometri yang paling mudah adalah berdasarkan pengetahuan dan keupayaan untuk menentukan pada bulatan trigonometri nilai bukan sahaja sudut trigonometri utama, tetapi juga nilai lain.
Sementara itu, penyelesaian ketaksamaan bentuk , , , boleh dijalankan seperti berikut: pertama, kita dapati beberapa selang () di mana ketaksamaan ini adalah benar, dan kemudian kita tulis jawapan akhir dengan menambah pada hujung yang dijumpai. selang gandaan tempoh sinus atau kosinus: ( 
). Dalam kes ini, nilai mudah dijumpai, kerana atau . Pencarian nilai bergantung pada gerak hati pelajar, keupayaan mereka untuk melihat kesamaan lengkok atau segmen, menggunakan simetri bahagian individu graf sinus atau kosinus. Dan ini kadangkala di luar kuasa bilangan pelajar yang agak ramai. Untuk mengatasi kesukaran yang dinyatakan dalam buku teks dalam beberapa tahun kebelakangan ini, pendekatan yang berbeza telah digunakan untuk menyelesaikan ketaksamaan trigonometri yang paling mudah, tetapi ini tidak meningkatkan hasil pembelajaran.
Selama beberapa tahun, kami telah agak berjaya menggunakan rumus punca-punca persamaan yang sepadan untuk mencari penyelesaian kepada ketaksamaan trigonometri.
Kami mengkaji topik ini dengan cara berikut:
1. Kami membina graf dan y \u003d a, dengan mengandaikan bahawa .
Kemudian kita tuliskan persamaan dan penyelesaiannya. Memberi n 0; satu; 2, kita dapati tiga punca persamaan tersusun: . Nilai-nilai adalah abscissas tiga titik persilangan berturut-turut bagi graf dan y = a. adalah jelas bahawa ketaksamaan sentiasa berlaku pada selang (), dan pada selang () - ketaksamaan .
Menambah pada hujung selang ini nombor yang merupakan gandaan tempoh sinus, dalam kes pertama kita memperoleh penyelesaian ketaksamaan dalam bentuk: ; dan dalam kes kedua, penyelesaian ketaksamaan dalam bentuk:
Hanya berbeza dengan sinus dari formula, yang merupakan penyelesaian kepada persamaan, untuk n = 0 kita mendapat dua punca, dan punca ketiga untuk n = 1 dalam bentuk 
. Dan sekali lagi ialah tiga absis berturut-turut bagi titik persilangan graf dan . Dalam selang () ketaksamaan dipenuhi, dalam selang () ketaksamaan
Sekarang adalah mudah untuk menulis penyelesaian bagi ketaksamaan dan . Dalam kes pertama, kita dapat: ;
dan dalam yang kedua: .
rumuskan. Untuk menyelesaikan ketaksamaan atau , adalah perlu untuk mengarang persamaan yang sepadan dan menyelesaikannya. Daripada formula yang terhasil, cari punca dan , dan tulis jawapan bagi ketaksamaan dalam bentuk: .
Apabila menyelesaikan ketaksamaan , daripada formula punca persamaan yang sepadan kita dapati punca dan , dan tulis jawapan ketaksamaan dalam bentuk: .
Teknik ini membolehkan anda mengajar semua pelajar cara menyelesaikan ketaksamaan trigonometri. teknik ini bergantung sepenuhnya kepada kemahiran yang telah dikuasai dengan kukuh oleh pelajar. Ini adalah keupayaan untuk menyelesaikan yang paling mudah dan mencari nilai pembolehubah menggunakan formula. Di samping itu, ia menjadi tidak perlu untuk menyelesaikan sebilangan besar latihan dengan teliti di bawah bimbingan seorang guru untuk menunjukkan semua jenis teknik penaakulan bergantung pada tanda ketaksamaan, nilai modulus nombor a dan tandanya. Dan proses menyelesaikan ketidaksamaan menjadi singkat dan, yang sangat penting, seragam.
Satu lagi kelebihan kaedah ini ialah ia memudahkan untuk menyelesaikan ketaksamaan walaupun bahagian kanan bukan nilai jadual sinus atau kosinus.
Mari kita tunjukkan ini dengan contoh khusus. Biarkan ia diperlukan untuk menyelesaikan ketaksamaan. Mari kita tulis persamaan yang sepadan dan selesaikannya:
Mari cari nilai dan .
Untuk n = 1 
Untuk n = 2 
Kami menulis jawapan akhir untuk ketidaksamaan ini:
Dalam contoh yang dipertimbangkan untuk menyelesaikan ketaksamaan trigonometri yang paling mudah, hanya terdapat satu kelemahan - kehadiran sejumlah formalisme. Tetapi jika segala-galanya dinilai hanya dari kedudukan ini, maka mungkin untuk menuduh formalisme kedua-dua formula akar persamaan kuadratik, dan semua formula untuk menyelesaikan persamaan trigonometri, dan banyak lagi.
Kaedah yang dicadangkan, walaupun ia menduduki tempat yang layak dalam pembentukan kemahiran dan kebolehan untuk menyelesaikan ketaksamaan trigonometri, seseorang tidak boleh memandang rendah kepentingan dan ciri kaedah lain untuk menyelesaikan ketaksamaan trigonometri. Ini termasuk kaedah selang.
Mari kita pertimbangkan intipatinya.
Set disunting oleh A.G. Mordkovich, walaupun buku teks lain juga tidak boleh diabaikan. § 3. Kaedah mengajar topik "Fungsi trigonometri" dalam kursus algebra dan permulaan analisis Dalam kajian fungsi trigonometri di sekolah, dua peringkat utama boleh dibezakan: ü Pengenalan awal dengan fungsi trigonometri ...
Tugas-tugas berikut telah diselesaikan semasa penyelidikan: 1) Buku teks semasa algebra dan permulaan analisis matematik telah dianalisis untuk mengenal pasti metodologi yang dibentangkan di dalamnya untuk menyelesaikan persamaan tidak rasional dan ketaksamaan. Analisis yang dijalankan membolehkan kita membuat kesimpulan berikut: Di sekolah menengah, perhatian yang tidak mencukupi diberikan kepada kaedah untuk menyelesaikan pelbagai persamaan tidak rasional, terutamanya ...
KAEDAH UNTUK MENYELESAIKAN KETIDAKSAMAAN TRIGONOMETRI
Perkaitan. Dari segi sejarah, persamaan trigonometri dan ketaksamaan telah diberi tempat yang istimewa dalam kurikulum sekolah. Kita boleh mengatakan bahawa trigonometri adalah salah satu bahagian yang paling penting dalam kursus sekolah dan semua sains matematik secara umum.
Persamaan trigonometri dan ketaksamaan menduduki salah satu tempat utama dalam kursus matematik sekolah menengah, baik dari segi kandungan bahan pendidikan dan kaedah aktiviti pendidikan dan kognitif yang boleh dan harus dibentuk semasa pengajian mereka dan digunakan untuk menyelesaikan masalah besar. bilangan masalah yang bersifat teori dan gunaan.
Penyelesaian persamaan dan ketaksamaan trigonometri mewujudkan prasyarat untuk mensistematikkan pengetahuan pelajar yang berkaitan dengan semua bahan pendidikan dalam trigonometri (contohnya, sifat fungsi trigonometri, kaedah untuk mengubah ungkapan trigonometri, dll.) dan memungkinkan untuk mewujudkan hubungan yang berkesan dengan bahan yang dikaji dalam algebra (persamaan, kesetaraan persamaan, ketaksamaan, transformasi serupa ungkapan algebra, dll.).
Dengan kata lain, pertimbangan kaedah untuk menyelesaikan persamaan trigonometri dan ketaksamaan melibatkan sejenis pemindahan kemahiran ini kepada kandungan baharu.
Kepentingan teori dan banyak aplikasinya adalah bukti perkaitan topik yang dipilih. Ini, seterusnya, membolehkan anda menentukan matlamat, objektif dan subjek penyelidikan kerja kursus.
Tujuan kajian: umumkan jenis ketaksamaan trigonometri yang ada, kaedah asas dan khas untuk penyelesaiannya, pilih satu set tugas untuk menyelesaikan ketaksamaan trigonometri oleh murid sekolah.
Objektif kajian:
1. Berdasarkan analisis literatur yang ada mengenai topik kajian, sistematikkan bahan tersebut.
2. Berikan satu set tugas yang perlu untuk menyatukan topik "Ketaksamaan trigonometri."
Objek kajian adalah ketaksamaan trigonometri dalam kursus matematik sekolah.
Subjek kajian: jenis ketaksamaan trigonometri dan kaedah penyelesaiannya.
Kepentingan teori adalah untuk menyusun bahan.
Kepentingan praktikal: aplikasi pengetahuan teori dalam menyelesaikan masalah; analisis kaedah utama yang sering ditemui untuk menyelesaikan ketaksamaan trigonometri.
Kaedah penyelidikan : analisis kesusasteraan saintifik, sintesis dan generalisasi pengetahuan yang diperoleh, analisis penyelesaian masalah, mencari kaedah optimum untuk menyelesaikan ketidaksamaan.
§satu. Jenis ketaksamaan trigonometri dan kaedah asas untuk penyelesaiannya
1.1. Ketaksamaan trigonometri termudah
Dua ungkapan trigonometri yang dihubungkan dengan tanda atau > dipanggil ketaksamaan trigonometri.
Untuk menyelesaikan ketaksamaan trigonometri bermakna mencari satu set nilai yang tidak diketahui termasuk dalam ketaksamaan, di mana ketidaksamaan itu dipenuhi.
Bahagian utama ketaksamaan trigonometri diselesaikan dengan mengurangkannya kepada menyelesaikan yang paling mudah:
Ini mungkin kaedah pemfaktoran, perubahan pembolehubah ( 
, 
dsb.), di mana ketidaksamaan biasa pertama kali diselesaikan, dan kemudian ketidaksamaan bentuk 
dan lain-lain, atau cara lain.
Ketaksamaan termudah diselesaikan dalam dua cara: menggunakan bulatan unit atau secara grafik.
biarlahf(x
ialah salah satu fungsi trigonometri asas. Untuk menyelesaikan ketidaksamaan 
ia cukup untuk mencari penyelesaiannya pada satu tempoh, i.e. pada mana-mana bahagian yang panjangnya sama dengan tempoh fungsif
x
. Kemudian penyelesaian ketaksamaan asal akan ditemuix
, serta nilai-nilai yang berbeza daripada yang ditemui oleh mana-mana nombor integer tempoh fungsi. Dalam kes ini, adalah mudah untuk menggunakan kaedah grafik.
Mari kita berikan contoh algoritma untuk menyelesaikan ketaksamaan 
(
) dan 
.
Algoritma untuk menyelesaikan ketaksamaan (
).
1. Merumus definisi sinus bagi suatu nomborx pada bulatan unit.
3. Pada paksi-y, tandakan satu titik dengan koordinata .
4. Melalui titik ini, lukis garis selari dengan paksi OX, dan tandakan titik persilangannya dengan bulatan.
5. Pilih lengkok bulatan, semua titik yang mempunyai ordinat kurang daripadaa .
6. Nyatakan arah pintasan (lawan arah jam) dan tulis jawapan dengan menambah tempoh fungsi pada hujung selang2πn
,
.
Algoritma untuk menyelesaikan ketaksamaan .
1. Merumus definisi tangen bagi suatu nomborx pada bulatan unit.
2. Lukiskan bulatan unit.
3. Lukiskan garis tangen dan tanda satu titik di atasnya dengan ordinata .
4. Sambungkan titik ini kepada asal dan tandakan titik persilangan segmen yang terhasil dengan bulatan unit.
5. Pilih lengkok bulatan, semua titik yang mempunyai ordinat pada garis tangen yang kurang daripadaa .
6. Tunjukkan arah traversal dan tulis jawapan, mengambil kira skop fungsi, menambah noktahpn
,
(nombor di sebelah kiri rekod sentiasa kurang daripada nombor di sebelah kanan).
Tafsiran grafik penyelesaian kepada persamaan dan formula termudah untuk menyelesaikan ketaksamaan dalam bentuk umum diberikan dalam lampiran (Lampiran 1 dan 2).
Contoh 1
Selesaikan ketidaksamaan 
.
Lukiskan garisan pada bulatan unit 
, yang memotong bulatan pada titik A dan B.
Semua nilaiy
pada selang NM lebih
, semua titik lengkok AMB memenuhi ketaksamaan ini. Pada semua sudut putaran, besar 
, tetapi lebih kecil 
,
akan mengambil nilai yang lebih besar daripada
(tetapi tidak lebih daripada satu).
Rajah 1
Oleh itu, penyelesaian ketaksamaan adalah semua nilai dalam selang 
, iaitu 
. Untuk mendapatkan semua penyelesaian ketidaksamaan ini, cukup untuk menambah pada hujung selang ini 
, di mana 
, iaitu 
,
.
Perhatikan bahawa nilai 
dan 
adalah punca-punca persamaan 
,
mereka. 
;
.
Jawapan: 
, .
1.2. Kaedah grafik
Dalam amalan, kaedah grafik untuk menyelesaikan ketaksamaan trigonometri selalunya berguna. Pertimbangkan intipati kaedah pada contoh ketidaksamaan 
:
1. Jika hujahnya rumit (berbeza denganX ), kemudian kami menggantikannya dengant .
2. Kami membina dalam satu satah koordinatmainan
graf fungsi 
dan 
.
3. Kami dapati sedemikiandua titik persilangan graf yang bersebelahan, antara yangsinusoidterletakdi atas
lurus . Cari absis bagi mata ini.
4. Tulis ketaksamaan berganda untuk hujaht , dengan mengambil kira tempoh kosinus (t akan berada di antara abscissas yang ditemui).
5. Lakukan penggantian terbalik (kembali kepada hujah asal) dan nyatakan nilainyaX daripada ketaksamaan berganda, kami menulis jawapan sebagai selang berangka.
Contoh 2 Selesaikan ketaksamaan: .
Apabila menyelesaikan ketaksamaan dengan kaedah grafik, adalah perlu untuk membina graf fungsi setepat mungkin. Mari kita ubah ketidaksamaan kepada bentuk:
Mari kita bina graf fungsi dalam satu sistem koordinat 
dan 
(Gamb. 2).
Rajah.2
Graf fungsi bersilang pada satu titikTAPI
dengan koordinat 
; 
. Di antara 
titik graf 
di bawah mata carta 
. Dan bila nilai fungsi adalah sama. sebab tu di 
.
Jawapan: 
.
1.3. Kaedah algebra
Selalunya, ketaksamaan trigonometri asal, dengan penggantian yang dipilih dengan baik, boleh dikurangkan kepada ketaksamaan algebra (rasional atau tidak rasional). Kaedah ini melibatkan mengubah ketaksamaan, memperkenalkan penggantian, atau menggantikan pembolehubah.
Mari kita pertimbangkan penggunaan kaedah ini pada contoh konkrit.
Contoh 3
Pengurangan kepada bentuk termudah 
.
(Gamb. 3)
Rajah.3
, 
.
Jawapan: 
,
Contoh 4 Selesaikan ketaksamaan:
ODZ: 
, 
.
Menggunakan formula: 
, 
kita tulis ketidaksamaan dalam bentuk: 
.
Atau, andaikan 
selepas transformasi mudah kita dapat
,
,
.
Menyelesaikan ketaksamaan terakhir dengan kaedah selang, kita memperoleh:
Rajah.4
, masing-masing 
. Kemudian daripada Rajah. 4 mengikut 
, di mana 
.
Rajah.5
Jawapan: 
, 
.
1.4. Kaedah jarak
Skim umum untuk menyelesaikan ketaksamaan trigonometri dengan kaedah selang:
Menggunakan formula trigonometri, pemfaktoran.
Cari titik putus dan sifar fungsi, letakkannya pada bulatan.
Ambil apa-apa perkaraKepada (tetapi tidak ditemui lebih awal) dan ketahui tanda produk. Jika hasil darab adalah positif, maka letakkan satu titik di luar bulatan unit pada sinar yang sepadan dengan sudut. Jika tidak, letakkan titik di dalam bulatan.
Jika satu titik berlaku bilangan kali genap, kami memanggilnya titik gandaan genap; jika bilangan kali ganjil, kami memanggilnya titik gandaan ganjil. Lukis lengkok seperti berikut: mulakan dari satu titikKepada , jika titik seterusnya ialah kepelbagaian ganjil, maka lengkok itu bersilang dengan bulatan pada titik ini, tetapi jika titik itu ialah kepelbagaian genap, maka ia tidak bersilang.
Lengkok di belakang bulatan adalah jurang positif; di dalam bulatan adalah selang negatif.
Contoh 5 Selesaikan ketidaksamaan
, 
.
Mata siri pertama: 
.
Mata siri kedua: 
.
Setiap titik berlaku bilangan kali ganjil, iaitu semua titik kepelbagaian ganjil.
Ketahui tanda produk di 
: . Kami menandakan semua titik pada bulatan unit (Rajah 6):
nasi. 6
Jawapan: 
, 
; 
, 
; 
, 
.
Contoh 6 . Selesaikan ketidaksamaan.
Penyelesaian:
Mari cari sifar bagi ungkapan itu .
Dapatkanaem :
,
;
, 
;
, 
;
, 
;
Pada bulatan unit, nilai siriX
1
diwakili oleh titik 
. SiriX
2
memberikan mata 
. SiriX
3
kita dapat dua mata 
. Akhirnya, satu siriX
4
akan mewakili mata 
. Kami meletakkan semua titik ini pada bulatan unit, menunjukkan dalam kurungan di sebelah setiap kepelbagaiannya.
Sekarang biarkan nombor 
akan sama. Kami membuat anggaran dengan tanda:
Jadi intinyaA
hendaklah dipilih pada rasuk yang membentuk sudut 
dengan rasukOh,
di luar bulatan unit. (Perhatikan bahawa rasuk tambahanO
A
ia tidak perlu ditunjukkan dalam gambar. titikA
dipilih lebih kurang.)
Sekarang dari titikA
kami melukis garis berterusan beralun secara berurutan ke semua titik yang ditanda. Dan pada titik garisan kami melepasi dari satu kawasan ke kawasan lain: jika ia berada di luar bulatan unit, maka ia akan melaluinya. Mendekati titik 
, garisan kembali ke kawasan dalam, kerana kepelbagaian titik ini adalah genap. Begitu juga pada titik 
(dengan kepelbagaian genap) garisan perlu diputar ke kawasan luar. Jadi, kami melukis gambar tertentu yang digambarkan dalam Rajah. 7. Ia membantu untuk menyerlahkan kawasan yang dikehendaki pada bulatan unit. Mereka ditandakan dengan "+".
Rajah.7
Jawapan akhir:
Catatan. Jika garisan beralun, selepas melintasi semua titik yang ditanda pada bulatan unit, tidak boleh dikembalikan ke titikA , tanpa melintasi bulatan di tempat "haram", ini bermakna ralat telah dibuat dalam penyelesaian, iaitu, bilangan akar ganjil telah ditinggalkan.
Jawab: .
§2. Satu set tugas untuk menyelesaikan ketaksamaan trigonometri
Dalam proses membangunkan keupayaan murid sekolah untuk menyelesaikan ketaksamaan trigonometri, 3 peringkat juga boleh dibezakan.
1. persediaan,
2. pembentukan kemahiran untuk menyelesaikan ketaksamaan trigonometri termudah;
3. pengenalan ketaksamaan trigonometri jenis lain.
Tujuan peringkat persediaan adalah perlu untuk membentuk kanak-kanak sekolah keupayaan untuk menggunakan bulatan atau graf trigonometri untuk menyelesaikan ketaksamaan, iaitu:
Keupayaan untuk menyelesaikan ketaksamaan mudah bentuk ,
, ,
,
menggunakan sifat-sifat fungsi sinus dan kosinus;
Keupayaan untuk membuat ketaksamaan berganda untuk lengkok bulatan berangka atau untuk lengkok graf fungsi;
Keupayaan untuk melakukan pelbagai transformasi ungkapan trigonometri.
Adalah disyorkan untuk melaksanakan peringkat ini dalam proses mensistematisasikan pengetahuan murid sekolah tentang sifat-sifat fungsi trigonometri. Cara utama boleh menjadi tugas yang ditawarkan kepada pelajar dan dilakukan sama ada di bawah bimbingan guru atau secara bebas, serta kemahiran yang diperoleh dalam menyelesaikan persamaan trigonometri.
Berikut adalah contoh tugas tersebut:
1
. Tandakan satu titik pada bulatan unit 
, jika
.
2.
Dalam suku apakah satah koordinat adalah titik , jika 
sama dengan: 
3.
Tandakan titik pada bulatan trigonometri , jika:
4. Bawa ungkapan kepada fungsi trigonometrisayakuarters.
a) 
,
b) 
,
dalam) 
5. Diberi lengkok MR.M - tengahsayasuku tahun,R - tengahIIsuku tahun ke. Hadkan nilai pembolehubaht untuk: (karang ketaksamaan berganda) a) arka MP; b) RM arka.
6. Tulis ketaksamaan berganda untuk bahagian graf yang dipilih:
nasi. satu
7.
Selesaikan ketaksamaan 
, 
, 
, 
.
8. Tukar ungkapan .
Pada peringkat kedua pembelajaran untuk menyelesaikan ketaksamaan trigonometri, kami boleh menawarkan cadangan berikut berkaitan dengan metodologi untuk mengatur aktiviti pelajar. Pada masa yang sama, adalah perlu untuk memberi tumpuan kepada kemahiran pelajar untuk bekerja dengan bulatan trigonometri atau graf, yang terbentuk semasa penyelesaian persamaan trigonometri yang paling mudah.
Pertama, adalah mungkin untuk memotivasikan kesesuaian mendapatkan kaedah umum untuk menyelesaikan ketaksamaan trigonometri termudah dengan merujuk, sebagai contoh, kepada ketaksamaan bentuk 
.
Menggunakan pengetahuan dan kemahiran yang diperoleh pada peringkat persediaan, pelajar akan membawa ketidaksamaan yang dicadangkan ke dalam borang 
, tetapi mungkin sukar untuk mencari satu set penyelesaian kepada ketidaksamaan yang terhasil, kerana adalah mustahil untuk menyelesaikannya hanya menggunakan sifat-sifat fungsi sinus. Kesukaran ini boleh dielakkan dengan merujuk kepada ilustrasi yang sesuai (penyelesaian persamaan secara grafik atau menggunakan bulatan unit).
Kedua, guru harus menarik perhatian pelajar kepada cara yang berbeza untuk menyelesaikan tugasan, memberikan contoh yang sesuai untuk menyelesaikan ketaksamaan secara grafik dan menggunakan bulatan trigonometri.
Pertimbangkan pilihan sedemikian untuk menyelesaikan ketidaksamaan .
1. Menyelesaikan ketaksamaan menggunakan bulatan unit.
Dalam pelajaran pertama tentang menyelesaikan ketaksamaan trigonometri, kami akan menawarkan pelajar algoritma penyelesaian terperinci, yang dalam pembentangan langkah demi langkah mencerminkan semua kemahiran asas yang diperlukan untuk menyelesaikan ketidaksamaan.
Langkah 1.Lukis bulatan unit, tandakan satu titik pada paksi-y 
dan lukis garis lurus melaluinya selari dengan paksi-x. Garis ini akan memotong bulatan unit pada dua titik. Setiap titik ini menggambarkan nombor yang sinusnya sama dengan .
Langkah 2Garis lurus ini membahagikan bulatan kepada dua lengkok. Mari kita pilih nombor yang memaparkan nombor yang mempunyai sinus lebih besar daripada . Sememangnya, lengkok ini terletak di atas garis lurus yang dilukis.
nasi. 2
Langkah 3Mari pilih salah satu hujung arka yang ditanda. Mari tuliskan salah satu nombor yang diwakili oleh titik bulatan unit ini 
.
Langkah 4Untuk memilih nombor yang sepadan dengan hujung kedua lengkok yang dipilih, kami "melepasi" sepanjang lengkok ini dari hujung yang dinamakan ke hujung yang lain. Pada masa yang sama, kita ingat bahawa apabila bergerak lawan jam, nombor yang akan kita lalui meningkat (apabila bergerak ke arah yang bertentangan, nombor akan berkurangan). Mari tuliskan nombor yang digambarkan pada bulatan unit pada hujung kedua lengkok yang ditanda 
.
Oleh itu, kita melihat bahawa ketidaksamaan memenuhi nombor yang ketidaksamaan 
. Kami menyelesaikan ketaksamaan untuk nombor yang terletak pada tempoh yang sama bagi fungsi sinus. Oleh itu, semua penyelesaian ketaksamaan boleh ditulis sebagai 
Pelajar harus diminta untuk mempertimbangkan dengan teliti angka itu dan memikirkan mengapa semua penyelesaian kepada ketidaksamaan boleh ditulis dalam bentuk 
, 
.
nasi. 3
Adalah perlu untuk menarik perhatian pelajar kepada fakta bahawa apabila menyelesaikan ketaksamaan untuk fungsi kosinus, kita melukis garis lurus selari dengan paksi-y.
Cara grafik untuk menyelesaikan ketidaksamaan.
Membina carta 
dan 
, memandangkan itu 
.
nasi. empat
Kemudian kita tulis persamaan 
dan keputusannya 
, 
, 
, didapati menggunakan formula 
, 
, 
.
(Memberin
nilai 0, 1, 2, kita dapati tiga punca persamaan tersusun). Nilai 
ialah tiga absis berturut-turut bagi titik persilangan graf dan . Jelas sekali, sentiasa dalam selang waktu 
ketidaksamaan itu 
, dan pada selang waktu 
- ketidaksamaan 
. Kami berminat dengan kes pertama, dan kemudian menambah pada hujung selang ini nombor yang merupakan gandaan tempoh sinus, kami memperoleh penyelesaian kepada ketaksamaan sebagai: 
, .
nasi. 5
rumuskan. Untuk menyelesaikan ketidaksamaan , anda perlu menulis persamaan yang sepadan dan menyelesaikannya. Daripada formula yang terhasil cari punca 
dan 
, dan tulis jawapan bagi ketaksamaan dalam bentuk: , .
Ketiga, fakta tentang set punca ketaksamaan trigonometri yang sepadan sangat jelas disahkan apabila menyelesaikannya secara grafik.
nasi. 6
Adalah perlu untuk menunjukkan kepada pelajar bahawa gegelung, yang merupakan penyelesaian kepada ketaksamaan, berulang melalui selang yang sama, sama dengan tempoh fungsi trigonometri. Anda juga boleh mempertimbangkan ilustrasi yang serupa untuk graf fungsi sinus.
Keempat, adalah dinasihatkan untuk menjalankan kerja untuk mengemas kini kaedah pelajar menukar jumlah (perbezaan) fungsi trigonometri kepada produk, untuk menarik perhatian pelajar sekolah kepada peranan teknik ini dalam menyelesaikan ketaksamaan trigonometri.
Kerja sedemikian boleh dianjurkan melalui pemenuhan bebas pelajar terhadap tugas yang dicadangkan oleh guru, antaranya kami menyerlahkan perkara berikut:
Kelima, pelajar mesti dikehendaki menggambarkan penyelesaian setiap ketaksamaan trigonometri mudah menggunakan graf atau bulatan trigonometri. Pastikan anda memberi perhatian kepada kesesuaiannya, terutamanya kepada penggunaan bulatan, kerana apabila menyelesaikan ketaksamaan trigonometri, ilustrasi yang sepadan berfungsi sebagai cara yang sangat mudah untuk menetapkan set penyelesaian kepada ketidaksamaan tertentu.
Pengenalan pelajar dengan kaedah untuk menyelesaikan ketaksamaan trigonometri, yang bukan yang paling mudah, hendaklah dijalankan mengikut skema berikut: merujuk kepada ketaksamaan trigonometri tertentu merujuk kepada persamaan trigonometri yang sepadan carian bersama (guru - pelajar) untuk pemindahan bebas penyelesaian daripada teknik yang ditemui kepada ketaksamaan lain daripada jenis yang sama.
Untuk mensistemkan pengetahuan pelajar tentang trigonometri, kami mengesyorkan secara khusus memilih ketidaksamaan sedemikian, penyelesaian yang memerlukan pelbagai transformasi yang boleh dilaksanakan dalam proses menyelesaikannya, memfokuskan perhatian pelajar pada ciri-ciri mereka.
Oleh kerana ketidaksamaan yang produktif, kami boleh mencadangkan, sebagai contoh, perkara berikut:
Sebagai kesimpulan, kami memberi contoh satu set masalah untuk menyelesaikan ketaksamaan trigonometri.
1. Selesaikan ketaksamaan:
2. Selesaikan ketaksamaan: 3. Cari semua penyelesaian ketaksamaan: 4. Cari semua penyelesaian ketaksamaan:a) 
, memenuhi syarat 
;
b) 
, memenuhi syarat 
.
5. Cari semua penyelesaian ketaksamaan:
a) ;
b) ;
dalam) 
;
G) 
;
e) 
.
6. Selesaikan ketaksamaan:
a) ;
b) ;
dalam);
G) 
;
e);
e);
dan) 
.
7. Selesaikan ketaksamaan:
a) 
;
b) ;
dalam);
G).
8. Selesaikan ketaksamaan:
a) ;
b) ;
dalam);
G) 
;
e) 
;
e);
dan) 
;
h).
Adalah dinasihatkan untuk menawarkan tugasan 6 dan 7 kepada pelajar yang mempelajari matematik di peringkat lanjutan, tugas 8 - kepada pelajar dalam kelas dengan kajian matematik yang mendalam.
§3. Kaedah khas untuk menyelesaikan ketaksamaan trigonometri
Kaedah khas untuk menyelesaikan persamaan trigonometri - iaitu kaedah yang hanya boleh digunakan untuk menyelesaikan persamaan trigonometri. Kaedah ini adalah berdasarkan penggunaan sifat fungsi trigonometri, serta penggunaan pelbagai formula dan identiti trigonometri.
3.1. Kaedah Sektor
Pertimbangkan kaedah sektor untuk menyelesaikan ketaksamaan trigonometri. Penyelesaian ketaksamaan bentuk 
, di manaP
(
x
)
danQ
(
x
)
– fungsi trigonometri rasional (sinus, kosinus, tangen dan kotangen memasukkannya secara rasional), sama seperti penyelesaian ketaksamaan rasional. Adalah mudah untuk menyelesaikan ketaksamaan rasional dengan kaedah selang pada paksi nyata. Analoginya dalam menyelesaikan ketaksamaan trigonometri rasional ialah kaedah sektor dalam bulatan trigonometri, untuksinx
dancosx
(
) atau separuh bulatan trigonometri untuktgx
danctgx
(
).
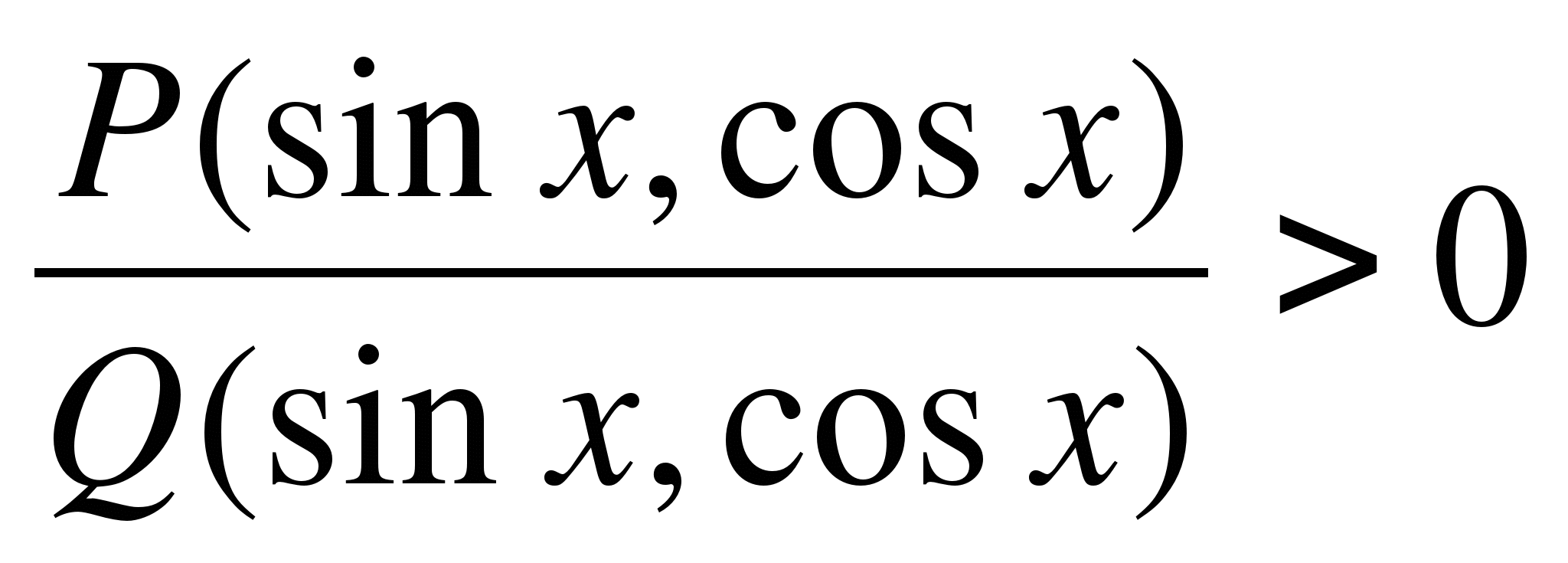
Dalam kaedah selang, setiap faktor linear pengangka dan penyebut bentuk 
titik pada paksi nombor 
, dan apabila melalui titik ini perubahan tanda. Dalam kaedah sektor, setiap pengganda bentuk 
, di mana 
- salah satu fungsisinx
ataucosx
dan 
, dalam bulatan trigonometri terdapat dua sudut yang sepadan 
dan 
, yang membahagikan bulatan kepada dua sektor. Apabila melalui dan fungsi perubahan tanda.
Perkara berikut mesti diingat:
a) Faktor bentuk 
dan 
, di mana 
, kekalkan tanda untuk semua nilai 
. Pengganda pembilang dan penyebut sedemikian dibuang, berubah (jika 
) bagi setiap penolakan tersebut, tanda ketidaksamaan diterbalikkan.
b) Pengganda bentuk 
dan 
juga dibuang. Selain itu, jika ini adalah faktor penyebut, maka ketaksamaan bentuk ditambah kepada sistem ketaksamaan yang setara. 
dan 
. Jika ini adalah faktor pengangka, maka dalam sistem kekangan yang setara ia sepadan dengan ketaksamaan dan dalam kes ketidaksamaan awal yang ketat, dan kesaksamaan 
dan 
dalam kes ketidaksamaan awal yang tidak ketat. Apabila menjatuhkan pengganda 
atau 
tanda ketidaksamaan diterbalikkan.
Contoh 1
Selesaikan ketaksamaan: a) 
, b) 
.
kita mempunyai fungsi, b). Selesaikan ketidaksamaan yang Kami ada
3.2. Kaedah bulatan sepusat
Kaedah ini adalah sama dengan kaedah paksi berangka selari dalam menyelesaikan sistem ketaksamaan rasional.
Pertimbangkan contoh sistem ketaksamaan.
Contoh 5
Selesaikan sistem ketaksamaan trigonometri mudah 
Pertama, kami menyelesaikan setiap ketidaksamaan secara berasingan (Rajah 5). Di sudut kanan atas rajah, kami akan menunjukkan hujah mana bulatan trigonometri dipertimbangkan.
Rajah.5
Seterusnya, kami membina sistem bulatan sepusat untuk hujahX . Kami melukis bulatan dan lorekkannya mengikut penyelesaian ketaksamaan pertama, kemudian kami lukis bulatan dengan jejari yang lebih besar dan lorekkannya mengikut penyelesaian kedua, kemudian kami membina bulatan untuk ketaksamaan ketiga dan bulatan asas . Kami melukis sinar dari pusat sistem melalui hujung lengkok supaya ia bersilang dengan semua bulatan. Kami membentuk penyelesaian pada bulatan asas (Rajah 6).
Rajah.6
Jawapan:
, 
.
Kesimpulan
Semua objektif kerja kursus telah selesai. Bahan teori disusun secara sistematik: jenis utama ketaksamaan trigonometri dan kaedah utama untuk penyelesaiannya (grafik, algebra, kaedah selang, sektor dan kaedah bulatan sepusat) diberikan. Bagi setiap kaedah, satu contoh penyelesaian ketaksamaan telah diberikan. Bahagian teori diikuti dengan bahagian praktikal. Ia mengandungi satu set tugas untuk menyelesaikan ketaksamaan trigonometri.
Kerja kursus ini boleh digunakan oleh pelajar untuk kerja bebas. Pelajar boleh menyemak tahap asimilasi topik ini, berlatih dalam melaksanakan tugasan yang mempunyai kerumitan yang berbeza-beza.
Setelah meneliti literatur yang relevan mengenai isu ini, jelas sekali, kita boleh menyimpulkan bahawa keupayaan dan kemahiran untuk menyelesaikan ketaksamaan trigonometri dalam kursus sekolah algebra dan permulaan analisis adalah sangat penting, pembangunannya memerlukan usaha yang besar di pihak guru matematik itu.
Oleh itu, kerja ini akan berguna untuk guru matematik, kerana ia memungkinkan untuk mengatur latihan pelajar dengan berkesan mengenai topik "Ketaksamaan trigonometri".
Kajian boleh diteruskan dengan mengembangkannya kepada kerja kelayakan akhir.
Senarai sastera terpakai
Bogomolov, N.V. Pengumpulan masalah dalam matematik [Teks] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 p.
Vygodsky, M.Ya. Buku panduan matematik asas [Teks] / M.Ya. Vygodsky. – M.: Bustard, 2006. – 509 p.
Zhurbenko, L.N. Matematik dalam contoh dan tugasan [Teks] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.
Ivanov, O.A. Matematik asas untuk pelajar sekolah, pelajar dan guru [Teks] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.
Karp, A.P. Tugas dalam algebra dan permulaan analisis untuk organisasi ulangan dan pensijilan akhir dalam gred ke-11 [Teks] / A.P. ikan mas. – M.: Pencerahan, 2005. – 79 p.
Kulanin, E.D. 3000 masalah persaingan dalam matematik [Teks] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.
Leibson, K.L. Koleksi tugas praktikal dalam matematik [Teks] / K.L. Leibson. – M.: Bustard, 2010. – 182 p.
Siku, V.V. Masalah dengan parameter dan penyelesaiannya. Trigonometri: persamaan, ketaksamaan, sistem. Gred 10 [Teks] / V.V. siku. – M.: ARKTI, 2008. – 64 p.
Manova, A.N. Matematik. Tutor ekspres untuk bersedia menghadapi peperiksaan: akaun. elaun [Teks] / A.N. Manova. - Rostov-on-Don: Phoenix, 2012. - 541 p.
Mordkovich, A.G. Algebra dan permulaan analisis matematik. 10-11 darjah. Buku teks untuk pelajar institusi pendidikan [Teks] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 p.
Novikov, A.I. Fungsi trigonometri, persamaan dan ketaksamaan [Teks] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 p.
Oganesyan, V.A. Kaedah pengajaran matematik di sekolah menengah: Metodologi am. Proc. elaun untuk pelajar fizik. - tikar. fak. ped. rakan seperjuangan. [Teks] / V.A. Oganesyan. – M.: Pencerahan, 2006. – 368 p.
Olechnik, S.N. Persamaan dan ketaksamaan. Kaedah penyelesaian bukan standard [Teks] / S.N. Olekhnik. - M .: Publishing House Factorial, 1997. - 219 hlm.
Sevryukov, P.F. Persamaan dan ketaksamaan trigonometri, eksponen dan logaritma [Teks] / P.F. Sevryukov. – M.: Pendidikan Negara, 2008. – 352 p.
Sergeev, I.N. GUNA: 1000 tugasan dengan jawapan dan penyelesaian dalam matematik. Semua tugas kumpulan C [Teks] / I.N. Sergeev. – M.: Peperiksaan, 2012. – 301 p.
Sobolev, A.B. Matematik asas [Teks] / A.B. Sobolev. - Yekaterinburg: GOU VPO USTU-UPI, 2005. - 81 p.
Fenko, L.M. Kaedah selang dalam menyelesaikan ketaksamaan dan mengkaji fungsi [Teks] / L.M. Fenko. – M.: Bustard, 2005. – 124 p.
Friedman, L.M. Asas teori metodologi pengajaran matematik [Teks] / L.M. Friedman. - M .: Rumah buku "LIBROKOM", 2009. - 248 p.
Lampiran 1
Tafsiran grafik penyelesaian kepada ketaksamaan yang paling mudah
nasi. satu
nasi. 2
Rajah.3
Rajah.4
Rajah.5
Rajah.6
Rajah.7
Rajah 8
Lampiran 2
Penyelesaian kepada ketidaksamaan yang paling mudah
