Double trigonometric inequalities. An algorithm for solving the simplest trigonometric inequalities and recognizing ways to solve trigonometric inequalities

- π - arcsin a + 2πn< t < arcsin a + 2πn, nєZ.

Apply it to the considered examples and you will get an answer much faster!

Conclusion: LEARN THE FORMULA, FRIENDS!

Page 1 of 1 1

1.5 Trigonometric inequalities and methods for their solution

1.5.1 Solving simple trigonometric inequalities

Most of the authors of modern textbooks on mathematics suggest that we begin our consideration of this topic by solving the simplest trigonometric inequalities. The principle of solving the simplest trigonometric inequalities is based on the knowledge and ability to determine on a trigonometric circle the values ​​​​of not only the main trigonometric angles, but also other values.

Meanwhile, the solution of inequalities of the form , , , can be carried out as follows: first we find some interval () on which this inequality is true, and then we write down the final answer by adding to the ends of the found interval a multiple of the period of the sine or cosine: ( ). In this case, the value is easily found, because or . The search for a value relies on the intuition of students, their ability to notice the equality of arcs or segments, using the symmetry of individual parts of the sine or cosine graph. And this is sometimes beyond the power of a fairly large number of students. In order to overcome the noted difficulties in textbooks in recent years, a different approach has been used to solve the simplest trigonometric inequalities, but this did not improve the learning outcomes.

For a number of years, we have been quite successfully using the formulas of the roots of the corresponding equations to find solutions to trigonometric inequalities.

We study this topic in the following way:

1. We build graphs and y \u003d a, assuming that .

Then we write down the equation and its solution. Giving n 0; one; 2, we find three roots of the composed equation: . The values ​​are the abscissas of three consecutive intersection points of the graphs and y = a. it is obvious that the inequality always holds on the interval (), and on the interval () - the inequality .

Adding to the ends of these intervals a number that is a multiple of the period of the sine, in the first case we obtain the solution of the inequality in the form: ; and in the second case, the solution of the inequality in the form:

Only in contrast to the sine from the formula, which is a solution to the equation, for n = 0 we get two roots, and the third root for n = 1 in the form . And again are three consecutive abscissas of the intersection points of the graphs and . In the interval () the inequality is fulfilled, in the interval () the inequality

Now it is easy to write down the solutions of the inequalities and . In the first case, we get: ;

and in the second: .

Summarize. To solve the inequality or , it is necessary to compose the corresponding equation and solve it. From the resulting formula, find the roots and , and write the answer of the inequality in the form: .

When solving inequalities , from the formula of the roots of the corresponding equation we find the roots and , and write the answer of the inequality in the form: .

This technique allows you to teach all students how to solve trigonometric inequalities. this technique relies entirely on the skills that students have firmly mastered. These are the ability to solve the simplest and find the value of a variable using a formula. In addition, it becomes completely optional to carefully solve a large number of exercises under the guidance of a teacher in order to demonstrate all kinds of reasoning techniques depending on the sign of inequality, the value of the modulus of the number a and its sign. And the very process of solving inequality becomes short and, which is very important, uniform.

Another advantage of this method is that it makes it easy to solve inequalities even when the right side is not a table value of sine or cosine.

Let's demonstrate this with a specific example. Let it be required to solve the inequality . Let's write the corresponding equation and solve it:

Let's find the values ​​of and .

For n = 1

For n = 2

We write the final answer to this inequality:

In the considered example of solving the simplest trigonometric inequalities, there can be only one drawback - the presence of a certain amount of formalism. But if everything is evaluated only from these positions, then it will be possible to accuse of formalism both the formulas of the roots of the quadratic equation, and all the formulas for solving trigonometric equations, and much more.

The proposed method, although it occupies a worthy place in the formation of skills and abilities for solving trigonometric inequalities, one cannot underestimate the importance and features of other methods for solving trigonometric inequalities. This includes the interval method.

Let's consider its essence.

Set edited by A.G. Mordkovich, although other textbooks should not be ignored either. § 3. Methods of teaching the topic "Trigonometric functions" in the course of algebra and the beginning of analysis In the study of trigonometric functions at school, two main stages can be distinguished: ü Initial acquaintance with trigonometric functions ...

The following tasks were solved during the research: 1) The current textbooks of algebra and the beginning of mathematical analysis were analyzed to identify the methods for solving irrational equations and inequalities presented in them. The analysis carried out allows us to draw the following conclusions: In high school, insufficient attention is paid to methods for solving various irrational equations, mainly ...

METHODS FOR SOLVING TRIGONOMETRIC INEQUALITIES

Relevance. Historically, trigonometric equations and inequalities have been given a special place in the school curriculum. We can say that trigonometry is one of the most important sections of the school course and of all mathematical science in general.

Trigonometric equations and inequalities occupy one of the central places in a high school mathematics course, both in terms of the content of the educational material and the methods of educational and cognitive activity that can and should be formed during their study and applied to solving a large number of problems of a theoretical and applied nature. .

The solution of trigonometric equations and inequalities creates the prerequisites for systematizing students' knowledge related to all educational material in trigonometry (for example, the properties of trigonometric functions, methods for transforming trigonometric expressions, etc.) and makes it possible to establish effective connections with the studied material in algebra (equations, equivalence of equations, inequalities, identical transformations of algebraic expressions, etc.).

In other words, the consideration of methods for solving trigonometric equations and inequalities involves a kind of transfer of these skills to a new content.

The significance of the theory and its numerous applications are proof of the relevance of the chosen topic. This, in turn, allows you to determine the goals, objectives and subject of research of the course work.

Purpose of the study: generalize the available types of trigonometric inequalities, basic and special methods for their solution, select a set of tasks for solving trigonometric inequalities by schoolchildren.

Research objectives:

1. Based on the analysis of the available literature on the research topic, systematize the material.

2. Give a set of tasks necessary to consolidate the topic "Trigonometric inequalities."

Object of study are trigonometric inequalities in the school mathematics course.

Subject of study: types of trigonometric inequalities and methods for their solution.

Theoretical significance is to organize the material.

Practical significance: application of theoretical knowledge in solving problems; analysis of the main frequently encountered methods for solving trigonometric inequalities.

Research methods : analysis of scientific literature, synthesis and generalization of the acquired knowledge, analysis of problem solving, search for optimal methods for solving inequalities.

§one. Types of trigonometric inequalities and basic methods for their solution

1.1. The simplest trigonometric inequalities

Two trigonometric expressions connected by a sign or > are called trigonometric inequalities.

To solve a trigonometric inequality means to find a set of values ​​of the unknowns included in the inequality, under which the inequality is satisfied.

The main part of trigonometric inequalities is solved by reducing them to solving the simplest ones:

This may be a method of factorization, change of variable (
,
etc.), where the usual inequality is first solved, and then the inequality of the form
etc., or other ways.

The simplest inequalities are solved in two ways: using the unit circle or graphically.

Let bef(x  is one of the basic trigonometric functions. To solve the inequality
it suffices to find its solution on one period, i.e. on any segment whose length is equal to the period of the functionf  x  . Then the solution of the original inequality will be all foundx , as well as those values ​​that differ from those found by any integer number of periods of the function. In this case, it is convenient to use the graphical method.

Let us give an example of an algorithm for solving inequalities
(
) and
.

Algorithm for solving the inequality
(
).

1. Formulate the definition of the sine of a numberx on the unit circle.

3. On the y-axis, mark a point with the coordinatea .

4. Through this point, draw a line parallel to the OX axis, and mark the points of intersection of it with the circle.

5. Select an arc of a circle, all points of which have an ordinate less thana .

6. Specify the direction of the bypass (counterclockwise) and write down the answer by adding the period of the function to the ends of the interval2πn ,
.

Algorithm for solving the inequality
.

1. Formulate the definition of the tangent of a numberx on the unit circle.

2. Draw a unit circle.

3. Draw a line of tangents and mark a point on it with an ordinatea .

4. Connect this point to the origin and mark the point of intersection of the resulting segment with the unit circle.

5. Select an arc of a circle, all points of which have an ordinate on the tangent line that is less thana .

6. Indicate the direction of the traversal and write down the answer, taking into account the scope of the function, adding a periodpn ,
(the number on the left side of the record is always less than the number on the right side).

Graphical interpretation of solutions to the simplest equations and formulas for solving inequalities in a general form are given in the appendix (Appendices 1 and 2).

Example 1 Solve the inequality
.

Draw a line on the unit circle
, which intersects the circle at points A and B.

All valuesy on the interval NM more , all points of the arc AMB satisfy this inequality. At all angles of rotation, large , but smaller ,
will take on values ​​greater than (but not more than one).

Fig.1

Thus, the solution of the inequality will be all values ​​in the interval
, i.e.
. In order to get all solutions of this inequality, it is enough to add to the ends of this interval
, where
, i.e.
,
. Note that the values
and
are the roots of the equation
,

those.
;
.

Answer:
,
.

1.2. Graphic method

In practice, a graphical method for solving trigonometric inequalities is often useful. Consider the essence of the method on the example of the inequality
:

1. If the argument is complex (different fromX ), then we replace it witht .

2. We build in one coordinate planetoOy function graphs
and
.

3. We find suchtwo adjacent points of intersection of graphs, between whichsinusoidlocatedhigher straight
. Find the abscissas of these points.

4. Write a double inequality for the argumentt , considering the cosine period (t will be between the found abscissas).

5. Do a reverse substitution (return to the original argument) and express the valueX from a double inequality, we write the answer as a numerical interval.

Example 2 Solve the inequality: .

When solving inequalities by a graphical method, it is necessary to build graphs of functions as accurately as possible. Let's transform the inequality to the form:

Let us construct graphs of functions in one coordinate system
and
(Fig. 2).

Fig.2

Function graphs intersect at a pointBUT with coordinates
;
. In between
graph points
below the chart points
. And when
function values ​​are the same. So
at
.

Answer:
.

1.3. Algebraic method

Quite often, the original trigonometric inequality, by a well-chosen substitution, can be reduced to an algebraic (rational or irrational) inequality. This method involves transforming the inequality, introducing a substitution, or replacing a variable.

Let's consider the application of this method on concrete examples.

Example 3 Reduction to the simplest form
.

(Fig. 3)

Fig.3

,
.

Answer:
,

Example 4 Solve the inequality:

ODZ:
,
.

Using formulas:
,

we write the inequality in the form:
.

Or, assuming
after simple transformations we get

,

,

.

Solving the last inequality by the interval method, we obtain:

Fig.4

, respectively
. Then from Fig. 4 follows
, where
.

Fig.5

Answer:
,
.

1.4. Spacing method

The general scheme for solving trigonometric inequalities by the interval method:

Using trigonometric formulas, factorize.

Find breakpoints and zeros of the function, put them on the circle.

Take any pointTo (but not found earlier) and find out the sign of the product. If the product is positive, then put a point outside the unit circle on the ray corresponding to the angle. Otherwise, put the point inside the circle.

If a point occurs an even number of times, we call it a point of even multiplicity; if an odd number of times, we call it a point of odd multiplicity. Draw arcs as follows: start from a pointTo , if the next point is of odd multiplicity, then the arc intersects the circle at this point, but if the point is of even multiplicity, then it does not intersect.

Arcs behind a circle are positive gaps; inside the circle are negative gaps.

Example 5 Solve the inequality

,
.

Points of the first series:
.

Points of the second series:
.

Each point occurs an odd number of times, that is, all points of odd multiplicity.

Find out the sign of the product at
: . We mark all points on the unit circle (Fig. 6):

Rice. 6

Answer:
,
;
,
;
,
.

Example 6 . Solve the inequality.

Decision:

Let's find the zeros of the expression .

Getaem :

,
;

,
;

,
;

,
;

On the unit circle, series valuesX 1 represented by dots
. SeriesX 2 gives points
. A seriesX 3 we get two points
. Finally, a seriesX 4 will represent points
. We put all these points on the unit circle, indicating in parentheses next to each of its multiplicity.

Now let the number will be equal. We make an estimate by the sign:

So the pointA should be chosen on the beam forming the angle with beamOh, outside the unit circle. (Note that the auxiliary beamO A it doesn't have to be shown in the picture. DotA selected approximately.)

Now from the pointA we draw a wavy continuous line sequentially to all the marked points. And at the points
our line passes from one region to another: if it was outside the unit circle, then it passes into it. Approaching the point , the line returns to the inner region, since the multiplicity of this point is even. Similarly at the point (with an even multiplicity) the line has to be rotated to the outer region. So, we drew a certain picture depicted in Fig. 7. It helps to highlight the desired areas on the unit circle. They are marked with a "+".

Fig.7

Final answer:

Note. If the wavy line, after traversing all the points marked on the unit circle, cannot be returned to the pointA , without crossing the circle in an “illegal” place, this means that an error was made in the solution, namely, an odd number of roots were omitted.

Answer: .

§2. A set of tasks for solving trigonometric inequalities

In the process of developing the ability of schoolchildren to solve trigonometric inequalities, 3 stages can also be distinguished.

1. preparatory,

2. formation of skills to solve the simplest trigonometric inequalities;

3. introduction of trigonometric inequalities of other types.

The purpose of the preparatory stage is that it is necessary to form in schoolchildren the ability to use a trigonometric circle or graph to solve inequalities, namely:

Ability to solve simple inequalities of the form
,
,
,
, using the properties of the sine and cosine functions;

Ability to make double inequalities for arcs of a numerical circle or for arcs of graphs of functions;

Ability to perform various transformations of trigonometric expressions.

It is recommended to implement this stage in the process of systematizing schoolchildren's knowledge about the properties of trigonometric functions. The main means can be tasks offered to students and performed either under the guidance of a teacher or independently, as well as skills gained in solving trigonometric equations.

Here are examples of such tasks:

1 . Mark a point on the unit circle , if

.

2. In what quarter of the coordinate plane is the point , if equals:

3. Mark points on the trigonometric circle , if:

4. Bring the expression to trigonometric functionsIquarters.

a)
, b)
, in)

5. Given the arc MR.M - middleIth quarter,R - middleIIth quarter. Restrict the value of a variablet for: (compose a double inequality) a) arc MP; b) RM arcs.

6. Write a double inequality for the selected sections of the graph:

Rice. one

7. Solve inequalities
,
,
,
.

8. Convert expression .

At the second stage of learning to solve trigonometric inequalities, we can offer the following recommendations related to the methodology for organizing students' activities. At the same time, it is necessary to focus on the students' skills to work with a trigonometric circle or a graph, which are formed during the solution of the simplest trigonometric equations.

First, it is possible to motivate the expediency of obtaining a general method for solving the simplest trigonometric inequalities by referring, for example, to an inequality of the form
. Using the knowledge and skills acquired at the preparatory stage, students will bring the proposed inequality to the form
, but may find it difficult to find a set of solutions to the resulting inequality, since it is impossible to solve it only using the properties of the sine function. This difficulty can be avoided by referring to the appropriate illustration (solution of the equation graphically or using a unit circle).

Secondly, the teacher should draw students' attention to different ways of completing the task, give an appropriate example of solving the inequality both graphically and using a trigonometric circle.

Consider such options for solving the inequality
.

1. Solving the inequality using the unit circle.

In the first lesson on solving trigonometric inequalities, we will offer students a detailed solution algorithm, which in a step-by-step presentation reflects all the basic skills necessary to solve the inequality.

Step 1.Draw a unit circle, mark a point on the y-axis and draw a straight line through it parallel to the x-axis. This line will intersect the unit circle at two points. Each of these points depicts numbers whose sine is equal to .

Step 2This straight line divided the circle into two arcs. Let's single out the one on which numbers are displayed that have a sine greater than . Naturally, this arc is located above the drawn straight line.

Rice. 2

Step 3Let's choose one of the ends of the marked arc. Let's write down one of the numbers that is represented by this point of the unit circle .

Step 4In order to choose a number corresponding to the second end of the selected arc, we "pass" along this arc from the named end to the other. At the same time, we recall that when moving counterclockwise, the numbers that we will pass increase (when moving in the opposite direction, the numbers would decrease). Let's write down the number that is depicted on the unit circle by the second end of the marked arc .

Thus, we see that the inequality
satisfy the numbers for which the inequality
. We solved the inequality for numbers located on the same period of the sine function. Therefore, all solutions of the inequality can be written as

Students should be asked to carefully consider the figure and figure out why all the solutions to the inequality
can be written in the form
,
.

Rice. 3

It is necessary to draw the attention of students to the fact that when solving inequalities for the cosine function, we draw a straight line parallel to the y-axis.

Graphical way to solve the inequality.

Building charts
and
, given that
.

Rice. 4

Then we write the equation
and his decision
,
,
, found using formulas
,
,
.

(Givingn values ​​0, 1, 2, we find three roots of the composed equation). Values
are three consecutive abscissas of the intersection points of the graphs
and
. Obviously, always on the interval
the inequality
, and on the interval
- inequality
. We are interested in the first case, and then adding to the ends of this interval a number that is a multiple of the sine period, we obtain a solution to the inequality
as:
,
.

Rice. 5

Summarize. To solve the inequality
, you need to write the corresponding equation and solve it. From the resulting formula find the roots and , and write the answer of the inequality in the form: ,
.

Thirdly, the fact about the set of roots of the corresponding trigonometric inequality is very clearly confirmed when solving it graphically.

Rice. 6

It is necessary to demonstrate to students that the coil, which is the solution to the inequality, repeats through the same interval, equal to the period of the trigonometric function. You can also consider a similar illustration for the graph of the sine function.

Fourthly, it is advisable to carry out work on updating the methods of converting the sum (difference) of trigonometric functions into a product among students, to draw the attention of schoolchildren to the role of these methods in solving trigonometric inequalities.

Such work can be organized through the students' independent fulfillment of the tasks proposed by the teacher, among which we highlight the following:

Fifth, students must be required to illustrate the solution of each simple trigonometric inequality using a graph or a trigonometric circle. Be sure to pay attention to its expediency, especially to the use of a circle, since when solving trigonometric inequalities, the corresponding illustration serves as a very convenient means of fixing the set of solutions to a given inequality.

Acquaintance of students with methods for solving trigonometric inequalities, which are not the simplest, should be carried out according to the following scheme: referring to a specific trigonometric inequality referring to the corresponding trigonometric equation joint search (teacher - students) for a solution independent transfer of the found technique to other inequalities of the same type.

In order to systematize students' knowledge of trigonometry, we recommend specifically selecting such inequalities, the solution of which requires various transformations that can be implemented in the process of solving it, focusing students' attention on their features.

As such productive inequalities, we can propose, for example, the following:

In conclusion, we give an example of a set of problems for solving trigonometric inequalities.

1. Solve the inequalities:

a)
, satisfying the condition
;

b)
, satisfying the condition
.

5. Find all solutions of inequalities:

a) ;

b) ;

in)
;

G)
;

e)
.

6. Solve the inequalities:

a) ;

b) ;

in) ;

G)
;

e) ;

e) ;

g)
.

7. Solve the inequalities:

a)
;

b) ;

in) ;

G) .

8. Solve the inequalities:

a) ;

b) ;

in) ;

G)
;

e)
;

e) ;

g)
;

h) .

It is advisable to offer tasks 6 and 7 to students studying mathematics at an advanced level, task 8 - to students in classes with in-depth study of mathematics.

§3. Special methods for solving trigonometric inequalities

Special methods for solving trigonometric equations - that is, those methods that can only be used to solve trigonometric equations. These methods are based on the use of the properties of trigonometric functions, as well as on the use of various trigonometric formulas and identities.

3.1. Sector Method

Consider the sector method for solving trigonometric inequalities. Solution of inequalities of the form

, whereP ( x ) andQ ( x ) - rational trigonometric functions (sines, cosines, tangents and cotangents enter them rationally), similarly to the solution of rational inequalities. It is convenient to solve rational inequalities by the method of intervals on the real axis. Its analogue in solving rational trigonometric inequalities is the method of sectors in a trigonometric circle, forsinx andcosx (
) or a trigonometric semicircle fortgx andctgx (
).

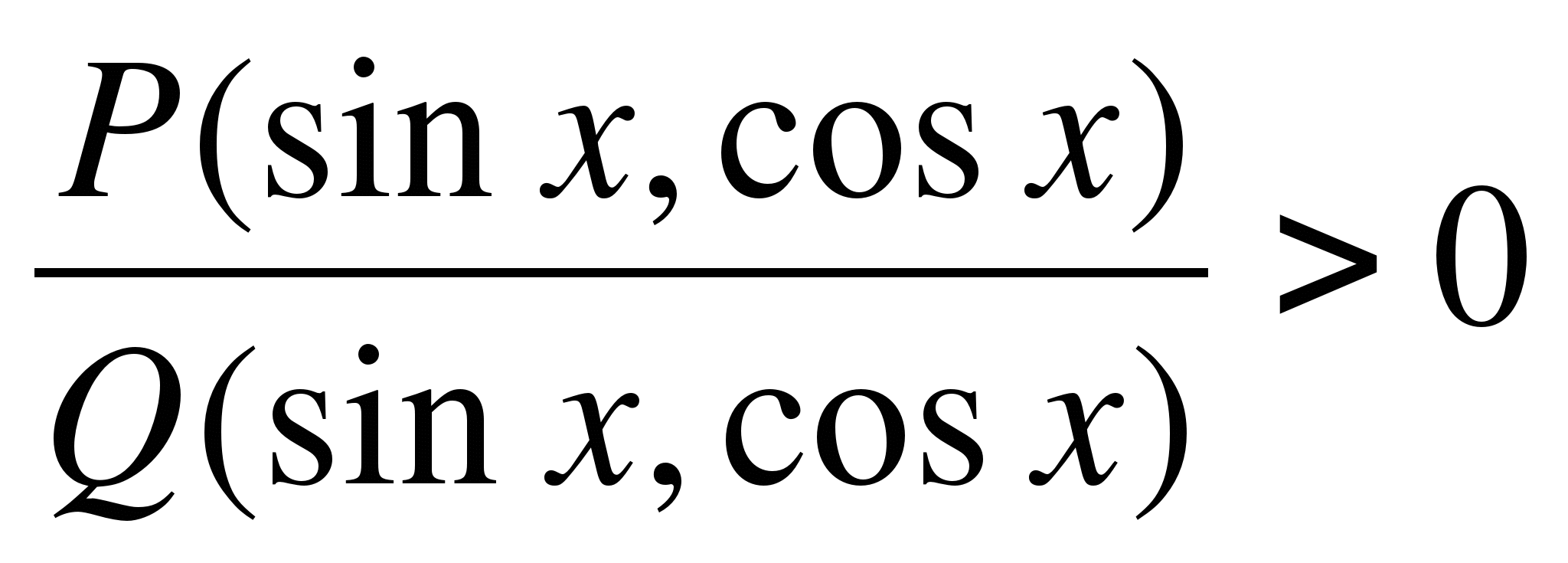
In the interval method, each linear factor of the numerator and denominator of the form
point on the number axis , and when passing through this point
changes sign. In the sector method, each multiplier of the form
, where
- one of the functionssinx orcosx and
, in a trigonometric circle there correspond two angles and
, which divide the circle into two sectors. When passing through and function
changes sign.

The following must be remembered:

a) Multipliers of the form
and
, where
, retain sign for all values . Such multipliers of the numerator and denominator are discarded, changing (if
) for each such rejection, the inequality sign is reversed.

b) Multipliers of the form
and
are also discarded. Moreover, if these are factors of the denominator, then inequalities of the form are added to the equivalent system of inequalities
and
. If these are factors of the numerator, then in the equivalent system of constraints they correspond to the inequalities
and
in the case of strict initial inequality, and equality
and
in the case of a non-strict initial inequality. When dropping the multiplier
or
the inequality sign is reversed.

Example 1 Solve inequalities: a)
, b)
. we have a function, b). Solve the inequality We have

3.2. Concentric circle method

This method is analogous to the method of parallel numerical axes in solving systems of rational inequalities.

Consider an example of a system of inequalities.

Example 5 Solve a system of simple trigonometric inequalities

First, we solve each inequality separately (Figure 5). In the upper right corner of the figure, we will indicate for which argument the trigonometric circle is considered.

Fig.5

Next, we build a system of concentric circles for the argumentX . We draw a circle and shade it according to the solution of the first inequality, then we draw a circle of a larger radius and shade it according to the solution of the second one, then we build a circle for the third inequality and a base circle. We draw rays from the center of the system through the ends of the arcs so that they intersect all circles. We form a solution on the base circle (Figure 6).

Fig.6

Answer:
,
.

Conclusion

All objectives of the coursework were completed. The theoretical material is systematized: the main types of trigonometric inequalities and the main methods for their solution (graphical, algebraic, method of intervals, sectors and the method of concentric circles) are given. For each method, an example of solving an inequality was given. The theoretical part was followed by the practical part. It contains a set of tasks for solving trigonometric inequalities.

This coursework can be used by students for independent work. Students can check the level of assimilation of this topic, practice in performing tasks of varying complexity.

Having worked through the relevant literature on this issue, obviously, we can conclude that the ability and skills to solve trigonometric inequalities in the school course of algebra and the beginning of analysis are very important, the development of which requires considerable effort on the part of the mathematics teacher.

Therefore, this work will be useful for teachers of mathematics, as it makes it possible to effectively organize the training of students on the topic "Trigonometric inequalities".

The study can be continued by expanding it to the final qualifying work.

List of used literature

Bogomolov, N.V. Collection of problems in mathematics [Text] / N.V. Bogomolov. – M.: Bustard, 2009. – 206 p.

Vygodsky, M.Ya. Handbook of elementary mathematics [Text] / M.Ya. Vygodsky. – M.: Bustard, 2006. – 509 p.

Zhurbenko, L.N. Mathematics in examples and tasks [Text] / L.N. Zhurbenko. – M.: Infra-M, 2009. – 373 p.

Ivanov, O.A. Elementary mathematics for schoolchildren, students and teachers [Text] / O.A. Ivanov. – M.: MTsNMO, 2009. – 384 p.

Karp, A.P. Tasks in algebra and the beginnings of analysis for the organization of the final repetition and certification in the 11th grade [Text] / A.P. Carp. – M.: Enlightenment, 2005. – 79 p.

Kulanin, E.D. 3000 competitive problems in mathematics [Text] / E.D. Kulanin. – M.: Iris-press, 2007. – 624 p.

Leibson, K.L. Collection of practical tasks in mathematics [Text] / K.L. Leibson. – M.: Bustard, 2010. – 182 p.

Elbow, V.V. Problems with parameters and their solution. Trigonometry: equations, inequalities, systems. Grade 10 [Text] / V.V. Elbow. – M.: ARKTI, 2008. – 64 p.

Manova, A.N. Mathematics. Express tutor to prepare for the exam: account. allowance [Text] / A.N. Manova. - Rostov-on-Don: Phoenix, 2012. - 541 p.

Mordkovich, A.G. Algebra and beginning of mathematical analysis. 10-11 grades. Textbook for students of educational institutions [Text] / A.G. Mordkovich. – M.: Iris-press, 2009. – 201 p.

Novikov, A.I. Trigonometric functions, equations and inequalities [Text] / A.I. Novikov. - M.: FIZMATLIT, 2010. - 260 p.

Oganesyan, V.A. Methods of teaching mathematics in secondary school: General methodology. Proc. allowance for physics students. - mat. fak. ped. in-comrade. [Text] / V.A. Oganesyan. – M.: Enlightenment, 2006. – 368 p.

Olechnik, S.N. Equations and inequalities. Non-standard solution methods [Text] / S.N. Olekhnik. - M .: Publishing House Factorial, 1997. - 219 p.

Sevryukov, P.F. Trigonometric, exponential and logarithmic equations and inequalities [Text] / P.F. Sevryukov. – M.: National Education, 2008. – 352 p.

Sergeev, I.N. USE: 1000 tasks with answers and solutions in mathematics. All tasks of group C [Text] / I.N. Sergeev. – M.: Exam, 2012. – 301 p.

Sobolev, A.B. Elementary mathematics [Text] / A.B. Sobolev. - Yekaterinburg: GOU VPO USTU-UPI, 2005. - 81 p.

Fenko, L.M. The method of intervals in solving inequalities and studying functions [Text] / L.M. Fenko. – M.: Bustard, 2005. – 124 p.

Friedman, L.M. Theoretical foundations of the methodology of teaching mathematics [Text] / L.M. Friedman. - M .: Book house "LIBROKOM", 2009. - 248 p.

Appendix 1

Graphical interpretation of solutions to the simplest inequalities

Rice. one

Rice. 2

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

Annex 2

Solutions to the simplest inequalities