5 complex numbers. Tutorial: Complex Numbers
Complex numbers
Imaginary And complex numbers. Abscissa and ordinate
complex number. Conjugate complex numbers.
Operations with complex numbers. Geometric
representation of complex numbers. Complex plane.
Modulus and argument of a complex number. Trigonometric
complex number form. Operations with complex
numbers in trigonometric form. Moivre's formula.
Basic information about imaginary And complex numbers are given in the section “Imaginary and complex numbers”. The need for these numbers of a new type arose when solving quadratic equations for the case
D< 0 (здесь D– discriminant of a quadratic equation). For a long time, these numbers did not find physical application, which is why they were called “imaginary” numbers. However, now they are very widely used in various fields of physics.and technology: electrical engineering, hydro- and aerodynamics, elasticity theory, etc.
Complex numbers are written in the form:a+bi. Here a And b – real numbers , A i – imaginary unit, i.e. e. i 2 = –1. Number a called abscissa,a b – ordinatecomplex numbera + bi.Two complex numbersa+bi And a–bi are called conjugate complex numbers.
Main agreements:
1. Real number
Acan also be written in the formcomplex number:a+ 0 i or a – 0 i. For example, records 5 + 0i and 5 – 0 imean the same number 5 .2. Complex number 0 + bicalled purely imaginary number. Recordbimeans the same as 0 + bi.
3. Two complex numbersa+bi Andc + diare considered equal ifa = c And b = d. Otherwise complex numbers are not equal.
Addition. Sum of complex numbersa+bi And c + diis called a complex number (a+c ) + (b+d ) i.Thus, when adding complex numbers, their abscissas and ordinates are added separately.
This definition corresponds to the rules for operations with ordinary polynomials.
Subtraction. The difference of two complex numbersa+bi(diminished) and c + di(subtrahend) is called a complex number (a–c ) + (b–d ) i.
Thus, When subtracting two complex numbers, their abscissas and ordinates are subtracted separately.
Multiplication. Product of complex numbersa+bi And c + di is called a complex number:
(ac–bd ) + (ad+bc ) i.This definition follows from two requirements:
1) numbers a+bi And c + dimust be multiplied like algebraic binomials,
2) number ihas the main property:i 2 = – 1.
EXAMPLE ( a+ bi )(a–bi) = a 2 + b 2 . Hence, work
two conjugate complex numbers is equal to the real
a positive number.
Division. Divide a complex numbera+bi (divisible) by anotherc + di(divider) - means to find the third numbere + f i(chat), which when multiplied by a divisorc + di, results in the dividenda + bi.
If the divisor is not zero, division is always possible.
EXAMPLE Find (8 +i ) : (2 – 3 i) .
Solution. Let's rewrite this ratio as a fraction:
Multiplying its numerator and denominator by 2 + 3i
AND Having performed all the transformations, we get:

Geometric representation of complex numbers. Real numbers are represented by points on the number line:
Here is the point Ameans the number –3, dotB– number 2, and O- zero. In contrast, complex numbers are represented by points on the coordinate plane. For this purpose, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see picture). This coordinate system is called complex plane .

Module complex number is the length of the vectorOP, representing a complex number on the coordinate ( comprehensive) plane. Modulus of a complex numbera+bi denoted | a+bi| or letter r
To solve problems with complex numbers, you need to understand the basic definitions. The main goal of this review article is to explain what complex numbers are and present methods for solving basic problems with complex numbers. So, a complex number will be called a number of the form z = a + bi, Where a, b- real numbers, which are called the real and imaginary parts of a complex number, respectively, and denote a = Re(z), b=Im(z).
i called the imaginary unit. i 2 = -1. In particular, any real number can be considered complex: a = a + 0i, where a is real. If a = 0 And b ≠ 0, then the number is usually called purely imaginary.
Now let's introduce operations on complex numbers.
Consider two complex numbers z 1 = a 1 + b 1 i And z 2 = a 2 + b 2 i.
Let's consider z = a + bi.

The set of complex numbers extends the set of real numbers, which in turn extends the set of rational numbers, etc. This chain of investments can be seen in the figure: N – natural numbers, Z – integers, Q – rational, R – real, C – complex. 
Representation of complex numbers
Algebraic notation.
Consider a complex number z = a + bi, this form of writing a complex number is called algebraic. We have already discussed this form of recording in detail in the previous section. The following visual drawing is used quite often 
Trigonometric form.
From the figure it can be seen that the number z = a + bi can be written differently. It's obvious that a = rcos(φ), b = rsin(φ), r=|z|, hence z = rcos(φ) + rsin(φ)i, φ ∈ (-π; π)
is called the argument of a complex number. This representation of a complex number is called trigonometric form. The trigonometric form of notation is sometimes very convenient. For example, it is convenient to use it to raise a complex number to an integer power, namely, if z = rcos(φ) + rsin(φ)i, That z n = r n cos(nφ) + r n sin(nφ)i, this formula is called Moivre's formula.
Demonstrative form.
Let's consider z = rcos(φ) + rsin(φ)i- a complex number in trigonometric form, write it in another form z = r(cos(φ) + sin(φ)i) = re iφ, the last equality follows from Euler’s formula, thus we have obtained a new form of writing a complex number: z = re iφ, which is called indicative. This form of notation is also very convenient for raising a complex number to a power: z n = r n e inφ, Here n not necessarily an integer, but can be an arbitrary real number. This form of notation is quite often used to solve problems.
Fundamental theorem of higher algebra
Let's imagine that we have a quadratic equation x 2 + x + 1 = 0. Obviously, the discriminant of this equation is negative and it has no real roots, but it turns out that this equation has two different complex roots. So, the fundamental theorem of higher algebra states that any polynomial of degree n has at least one complex root. It follows from this that any polynomial of degree n has exactly n complex roots, taking into account their multiplicity. This theorem is a very important result in mathematics and is widely used. A simple corollary of this theorem is that there are exactly n different roots of degree n of unity.
Main types of tasks
This section will look at the main types of simple problems involving complex numbers. Conventionally, problems involving complex numbers can be divided into the following categories.
- Performing simple arithmetic operations on complex numbers.
- Finding the roots of polynomials in complex numbers.
- Raising complex numbers to powers.
- Extracting roots from complex numbers.
- Using complex numbers to solve other problems.
Now let's look at general methods for solving these problems.
The simplest arithmetic operations with complex numbers are performed according to the rules described in the first section, but if complex numbers are presented in trigonometric or exponential forms, then in this case you can convert them into algebraic form and perform operations according to known rules.
Finding the roots of polynomials usually comes down to finding the roots of a quadratic equation. Suppose that we have a quadratic equation, if its discriminant is non-negative, then its roots will be real and can be found according to a well-known formula. If the discriminant is negative, that is, D = -1∙a 2, Where a is a certain number, then the discriminant can be represented as D = (ia) 2, hence √D = i|a|, and then you can use the already known formula for the roots of a quadratic equation.
Example. Let's return to the quadratic equation mentioned above x 2 + x + 1 = 0.
Discriminant - D = 1 - 4 ∙ 1 = -3 = -1(√3) 2 = (i√3) 2.
Now we can easily find the roots: 
Raising complex numbers to powers can be done in several ways. If you need to raise a complex number in algebraic form to a small power (2 or 3), then you can do this by direct multiplication, but if the power is larger (in problems it is often much larger), then you need to write this number in trigonometric or exponential forms and use already known methods.
Example. Consider z = 1 + i and raise it to the tenth power.
Let's write z in exponential form: z = √2 e iπ/4.
Then z 10 = (√2 e iπ/4) 10 = 32 e 10iπ/4.
Let's return to algebraic form: z 10 = -32i.
Extracting roots from complex numbers is the inverse operation of exponentiation and is therefore performed in a similar way. To extract roots, the exponential form of writing a number is often used.
Example. Let's find all roots of degree 3 of unity. To do this, we will find all the roots of the equation z 3 = 1, we will look for the roots in exponential form.
Let's substitute into the equation: r 3 e 3iφ = 1 or r 3 e 3iφ = e 0 .
Hence: r = 1, 3φ = 0 + 2πk, therefore φ = 2πk/3.
Different roots are obtained at φ = 0, 2π/3, 4π/3.
Therefore 1, e i2π/3, e i4π/3 are roots.
Or in algebraic form: 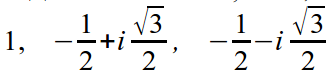
The last type of problems includes a huge variety of problems and there are no general methods for solving them. Let's give a simple example of such a task:
Find the amount sin(x) + sin(2x) + sin(2x) + … + sin(nx).
Although the formulation of this problem does not involve complex numbers, it can be easily solved with their help. To solve it, the following representations are used: 
If we now substitute this representation into the sum, then the problem is reduced to summing the usual geometric progression.
Conclusion
Complex numbers are widely used in mathematics; this review article examined the basic operations on complex numbers, described several types of standard problems and briefly described general methods for solving them; for a more detailed study of the capabilities of complex numbers, it is recommended to use specialized literature.
Literature
Let us recall the necessary information about complex numbers.
Complex number is an expression of the form a + bi, Where a, b are real numbers, and i- so-called imaginary unit, a symbol whose square is equal to –1, that is i 2 = –1. Number a called real part, and the number b - imaginary part complex number z = a + bi. If b= 0, then instead a + 0i they simply write a. It can be seen that real numbers are a special case of complex numbers.
Arithmetic operations on complex numbers are the same as on real numbers: they can be added, subtracted, multiplied and divided by each other. Addition and subtraction occur according to the rule ( a + bi) ± ( c + di) = (a ± c) + (b ± d)i, and multiplication follows the rule ( a + bi) · ( c + di) = (ac – bd) + (ad + bc)i(here it is used that i 2 = –1). Number = a – bi called complex conjugate To z = a + bi. Equality z · = a 2 + b 2 allows you to understand how to divide one complex number by another (non-zero) complex number:
(For example, ![]() .)
.)

Complex numbers have a convenient and visual geometric representation: number z = a + bi can be represented by a vector with coordinates ( a; b) on the Cartesian plane (or, which is almost the same thing, a point - the end of a vector with these coordinates). In this case, the sum of two complex numbers is depicted as the sum of the corresponding vectors (which can be found using the parallelogram rule). According to the Pythagorean theorem, the length of the vector with coordinates ( a; b) is equal to . This quantity is called module complex number z = a + bi and is denoted by | z|. The angle that this vector makes with the positive direction of the x-axis (counted counterclockwise) is called argument complex number z and is denoted by Arg z. The argument is not uniquely defined, but only up to the addition of a multiple of 2 π
radians (or 360°, if counted in degrees) - after all, it is clear that a rotation by such an angle around the origin will not change the vector. But if the vector of length r forms an angle φ
with the positive direction of the x-axis, then its coordinates are equal to ( r cos φ
; r sin φ
). From here it turns out trigonometric notation complex number: z = |z| · (cos(Arg z) + i sin(Arg z)). It is often convenient to write complex numbers in this form, because it greatly simplifies the calculations. Multiplying complex numbers in trigonometric form is very simple: z 1 · z 2 = |z 1 | · | z 2 | · (cos(Arg z 1 + Arg z 2) + i sin(Arg z 1 + Arg z 2)) (when multiplying two complex numbers, their modules are multiplied and their arguments are added). From here follow Moivre's formulas: z n = |z|n· (cos( n· (Arg z)) + i sin( n· (Arg z))). Using these formulas, it is easy to learn how to extract roots of any degree from complex numbers. nth root of z- this is a complex number w, What w n = z. It's clear that ![]() , And where k can take any value from the set (0, 1, ..., n- 1). This means that there is always exactly n roots n th degree of a complex number (on the plane they are located at the vertices of the regular n-gon).
, And where k can take any value from the set (0, 1, ..., n- 1). This means that there is always exactly n roots n th degree of a complex number (on the plane they are located at the vertices of the regular n-gon).
§ 1. Complex numbers: definitions, geometric interpretation, actions in algebraic, trigonometric and exponential forms
Definition of a complex number
Complex equalities
Geometric representation of complex numbers
Modulus and argument of a complex number
Algebraic and trigonometric forms of a complex number
Exponential form of a complex number
Euler's formulas
§ 2. Entire functions (polynomials) and their basic properties. Solving algebraic equations on the set of complex numbers
Definition of an algebraic equation of the th degree
Basic properties of polynomials
Examples of solving algebraic equations on the set of complex numbers
Self-test questions
Glossary
§ 1. Complex numbers: definitions, geometric interpretation, actions in algebraic, trigonometric and exponential forms
Definition of a complex number ( State the definition of a complex number)
A complex number z is an expression of the following form:
Complex number in algebraic form,(1)
Where x, y Î;
- complex conjugate number number z ;
- opposite number number z ;
- complex zero ;
– this is how the set of complex numbers is denoted.
1)z = 1 + iÞRe z= 1, Im z = 1, = 1 – i, = –1 – i ;
2)z = –1 + iÞRe z= –1, Im z = , = –1 – i, = –1 –i ;
3)z = 5 + 0i= 5 Þ Re z= 5, Im z = 0, = 5 – 0i = 5, = –5 – 0i = –5
Þ if Im z= 0, then z = x- real number;
4)z = 0 + 3i = 3iÞRe z= 0, Im z = 3, = 0 – 3i = –3i , = –0 – 3i = – 3i
Þ if Re z= 0, then z = iy - purely imaginary number.
Complex equalities (Formulate the meaning of complex equality)
1)  ;
;
2) .
.
One complex equality is equivalent to a system of two real equalities. These real equalities are obtained from complex equality by separating the real and imaginary parts.
1) ![]() ;
;
2) ![]() .
.
Geometric representation of complex numbers ( What is the geometric representation of complex numbers?)

Complex number z represented by a dot ( x , y) on the complex plane or the radius vector of this point.
Sign z in the second quarter means that the Cartesian coordinate system will be used as a complex plane.
Modulus and argument of a complex number ( What is the modulus and argument of a complex number?)
The modulus of a complex number is a non-negative real number
![]() .(2)
.(2)
Geometrically, the modulus of a complex number is the length of the vector representing the number z, or polar radius of a point ( x , y).
Draw the following numbers on the complex plane and write them in trigonometric form.
1)z = 1 + i Þ
![]() ,
,
Þ ![]()
Þ ![]() ;
;

![]() ,
,
Þ ![]()
Þ ![]() ;
;

![]() ,
,


5)![]() ,
,

that is, for z = 0 it will be
, j indefined.
Arithmetic operations on complex numbers (Give definitions and list the main properties of arithmetic operations on complex numbers.)
Addition (subtraction) of complex numbers
z 1 ± z 2 = (x 1 + iy 1) ± ( x 2 + iy 2) = (x 1 ± x 2) + i (y 1 ± y 2),(5)
that is, when adding (subtracting) complex numbers, their real and imaginary parts are added (subtracted).
1)(1 + i) + (2 – 3i) = 1 + i + 2 –3i = 3 – 2i ;
2)(1 + 2i) – (2 – 5i) = 1 + 2i – 2 + 5i = –1 + 7i .
Basic properties of addition
1)z 1 + z 2 = z 2 + z 1;
2)z 1 + z 2 + z 3 = (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3);
3)z 1 – z 2 = z 1 + (– z 2);
4)z + (–z) = 0;
Multiplying complex numbers in algebraic form
z 1∙z 2 = (x 1 + iy 1)∙(x 2 + iy 2) = x 1x 2 + x 1iy 2 + iy 1x 2 + i 2y 1y 2 = (6)
= (x 1x 2 – y 1y 2) + i (x 1y 2 + y 1x 2),
that is, the multiplication of complex numbers in algebraic form is carried out according to the rule of algebraic multiplication of a binomial by a binomial, followed by replacement and reduction of similar ones in real and imaginary terms.
1)(1 + i)∙(2 – 3i) = 2 – 3i + 2i – 3i 2 = 2 – 3i + 2i + 3 = 5 – i ;
2)(1 + 4i)∙(1 – 4i) = 1 – 42 i 2 = 1 + 16 = 17;
3)(2 + i)2 = 22 + 4i + i 2 = 3 + 4i .
Multiplying complex numbers in trigonometric form
z 1∙z 2 = r 1(cos j 1 + i sin j 1)× r 2(cos j 2 + i sin j 2) =
= r 1r 2(cos j 1cos j 2 + i cos j 1sin j 2 + i sin j 1cos j 2 + i 2 sin j 1sin j 2) =
= r 1r 2((cos j 1cos j 2 – sin j 1sin j 2) + i(cos j 1sin j 2 + sin j 1cos j 2))
The product of complex numbers in trigonometric form, that is, when multiplying complex numbers in trigonometric form, their modules are multiplied and their arguments are added.

Basic properties of multiplication
1)z 1× z 2 = z 2× z 1 - commutativity;
2)z 1× z 2× z 3 = (z 1× z 2)× z 3 = z 1×( z 2× z 3) - associativity;
3)z 1×( z 2 + z 3) = z 1× z 2 + z 1× z 3 - distributivity with respect to addition;
4)z×0 = 0; z×1 = z ;
Division of complex numbers
Division is the inverse operation of multiplication, so
If z × z 2 = z 1 and z 2 ¹ 0, then .
When performing division in algebraic form, the numerator and denominator of the fraction are multiplied by the complex conjugate of the denominator:
 Division of complex numbers in algebraic form.(7)
Division of complex numbers in algebraic form.(7)
When performing division in trigonometric form, the modules are divided and the arguments are subtracted:
 Dividing complex numbers in trigonometric form.(8)
Dividing complex numbers in trigonometric form.(8)
2) .
.
Raising a complex number to a natural power
It is more convenient to perform exponentiation in trigonometric form:
![]()
Moivre's formula, (9)
that is, when a complex number is raised to a natural power, its modulus is raised to this power, and the argument is multiplied by the exponent.
Calculate (1 + i)10.

Notes
1. When performing the operations of multiplication and raising to a natural power in trigonometric form, angle values beyond one full revolution can be obtained. But they can always be reduced to angles or by dropping an integer number of full revolutions using the periodicity properties of the functions and .
2. Meaning ![]() called the principal value of the argument of a complex number;
called the principal value of the argument of a complex number;
in this case, the values of all possible angles are denoted by ;
it's obvious that , .
Extracting the root of a natural degree from a complex number
 Euler's formulas(16)
Euler's formulas(16)
for which trigonometric functions and a real variable are expressed through an exponential function (exponent) with a purely imaginary exponent.
§ 2. Entire functions (polynomials) and their basic properties. Solving algebraic equations on the set of complex numbers
Two polynomials of the same degree n are identically equal to each other if and only if their coefficients coincide for the same powers of the variable x, that is
Proof
w Identity (3) is valid for "xО (or "xО)
Þ it is valid for ; substituting , we get an = bn .
Let us mutually cancel the terms in (3) an And bn and divide both parts by x :
This identity is also true for " x, including when x = 0
Þ assuming x= 0, we get an – 1 = bn – 1.
Let us mutually cancel the terms in (3") an– 1 and a n– 1 and divide both sides by x, as a result we get
Continuing the reasoning similarly, we obtain that an – 2 = bn –2, …, A 0 = b 0.
Thus, it has been proven that the identical equality of 2-x polynomials implies the coincidence of their coefficients at the same degrees x .
The converse statement is rightly obvious, i.e. if two polynomials have the same coefficients, then they are identical functions, therefore, their values coincide for all values of the argument, which means they are identically equal. Property 1 has been completely proven. v
When dividing a polynomial Pn (x) by the difference ( x – X 0) the remainder is equal to Pn (x 0), that is
![]() Bezout's theorem,(4)
Bezout's theorem,(4)
Where Qn – 1(x) - the integer part of division, is a polynomial of degree ( n – 1).
Proof
w Let's write the division formula with a remainder:
Pn (x) = (x – X 0)∙Qn – 1(x) + A ,
Where Qn – 1(x) - polynomial of degree ( n – 1),
A- the remainder, which is a number due to the well-known algorithm for dividing a polynomial by a binomial “in a column”.
This equality is true for " x, including when x = X 0 Þ
Pn (x 0) = (x 0 – x 0)× Qn – 1(x 0) + A Þ
A = Pn (X 0), etc. v
Corollary to Bezout's theorem. On dividing a polynomial by a binomial without a remainder
If the number X 0 is the zero of a polynomial, then this polynomial is divided by the difference ( x – X 0) without remainder, that is
Þ ![]() .(5)
.(5)
1) , since P 3(1) º 0
2) because P 4(–2) º 0
3) because P 2(–1/2) º 0
Dividing polynomials into binomials “in a column”:
| _ | _ | |||||||||||||
| _ | _ | |||||||||||||
| _ | ||||||||||||||
Every polynomial of degree n ³ 1 has at least one zero, real or complex
The proof of this theorem is beyond the scope of our course. Therefore, we accept the theorem without proof.
Let's work on this theorem and Bezout's theorem with the polynomial Pn (x).
After n-multiple application of these theorems we obtain that
Where a 0 is the coefficient at x n V Pn (x).
Corollary to the fundamental theorem of algebra. On the decomposition of a polynomial into linear factors
Any polynomial of degree on the set of complex numbers can be decomposed into n linear factors, that is
Expansion of a polynomial into linear factors, (6)
where x1, x2, ... xn are the zeros of the polynomial.
Moreover, if k numbers from the set X 1, X 2, … xn coincide with each other and with the number a, then in the product (6) the multiplier ( x– a) k. Then the number x= a is called k-fold zero of the polynomial Pn ( x) . If k= 1, then zero is called simple zero of the polynomial Pn ( x) .
1)P 4(x) = (x – 2)(x– 4)3 Þ x 1 = 2 - simple zero, x 2 = 4 - triple zero;
2)P 4(x) = (x – i)4 Þ x = i- zero multiplicity 4.
Property 4 (about the number of roots of an algebraic equation)
Any algebraic equation Pn(x) = 0 of degree n has exactly n roots on the set of complex numbers, if we count each root as many times as its multiplicity.
1)x 2 – 4x+ 5 = 0 - algebraic equation of the second degree
Þ x 1.2 = 2 ± = 2 ± i- two roots;
2)x 3 + 1 = 0 - algebraic equation of the third degree
Þ x
1,2,3 =  - three roots;
- three roots;
3)P 3(x) = x 3 + x 2 – x– 1 = 0 Þ x 1 = 1, because P 3(1) = 0.
Divide the polynomial P 3(x) on ( x – 1):
| x 3 | + | x 2 | – | x | – | 1 | x – 1 |
| x 3 | – | x 2 | x 2 + 2x +1 | ||||
| 2x 2 | – | x | |||||
| 2x 2 | – | 2x | |||||
| x | – | 1 | |||||
| x | – | 1 | |||||
| 0 |
Original equation
P 3(x) = x 3 + x 2 – x– 1 = 0 Û( x – 1)(x 2 + 2x+ 1) = 0 Û( x – 1)(x + 1)2 = 0
Þ x 1 = 1 - simple root, x 2 = –1 - double root.
1) – paired complex conjugate roots;
Any polynomial with real coefficients is decomposed into the product of linear and quadratic functions with real coefficients.
Proof
w Let x 0 = a + bi- zero of a polynomial Pn (x). If all the coefficients of this polynomial are real numbers, then it is also zero (by property 5).
Let's calculate the product of binomials ![]() :
:
complex number polynomial equation
Got ( x – a)2 + b 2 - square trinomial with real coefficients.
Thus, any pair of binomials with complex conjugate roots in formula (6) leads to a quadratic trinomial with real coefficients. v
1)P 3(x) = x 3 + 1 = (x + 1)(x 2 – x + 1);
2)P 4(x) = x 4 – x 3 + 4x 2 – 4x = x (x –1)(x 2 + 4).
Examples of solving algebraic equations on the set of complex numbers ( Give examples of solving algebraic equations on the set of complex numbers)
1. Algebraic equations of the first degree:
, is the only simple root.
2. Quadratic equations:
![]() ,
, ![]() – always has two roots (different or equal).
– always has two roots (different or equal).
1) ![]() .
.
3. Binomial equations of degree:
, – always has different roots.
![]() ,
,
Answer: , ![]() .
.
4. Solve the cubic equation.
An equation of the third degree has three roots (real or complex), and you need to count each root as many times as its multiplicity. Since all the coefficients of this equation are real numbers, the complex roots of the equation, if any, will be pair complex conjugates.
By selection we find the first root of the equation, since .
By corollary to Bezout's theorem. We calculate this division “in a column”:
| _ | |||||
| _ | |||||
| _ | |||||
Now representing the polynomial as a product of a linear and a square factor, we get:
![]() .
.
We find other roots as roots of a quadratic equation: ![]()
Answer: , ![]() .
.
5. Construct an algebraic equation of the smallest degree with real coefficients, if it is known that the numbers x 1 = 3 and x 2 = 1 + i are its roots, and x 1 is a double root, and x 2 - simple.
The number is also the root of the equation, because the coefficients of the equation must be real.
In total, the required equation has 4 roots: x 1, x 1,x 2, . Therefore, its degree is 4. We compose a polynomial of the 4th degree with zeros x
11. What is a complex zero?
13. Formulate the meaning of complex equality.
15. What is the modulus and argument of a complex number?
17. What is the argument of a complex number?
18. What is the name or meaning of the formula?
19. Explain the meaning of the notation in this formula:
27. Give definitions and list the main properties of arithmetic operations on complex numbers.
28. What is the name or meaning of the formula?
29. Explain the meaning of the notation in this formula:
31. What is the name or meaning of the formula?
32. Explain the meaning of the notation in this formula:
34. What is the name or meaning of the formula?
35. Explain the meaning of the notation in this formula:
61. List the main properties of polynomials.
63. State the property about dividing a polynomial by the difference (x – x0).
65. What is the name or meaning of the formula?
66. Explain the meaning of the notation in this formula:
67. ⌂ ![]() .
.
69. State the theorem: the fundamental theorem of algebra.
70. What is the name or meaning of the formula?
71. Explain the meaning of the notation in this formula:
75. State the property about the number of roots of an algebraic equation.
78. State the property about the decomposition of a polynomial with real coefficients into linear and quadratic factors.
Glossary
The k-fold zero of a polynomial is... (p. 18)
an algebraic polynomial is called... (p. 14)
an algebraic equation of the nth degree is called... (p. 14)
the algebraic form of a complex number is called... (p. 5)
the argument of a complex number is... (page 4)
the real part of a complex number z is... (page 2)
a complex conjugate number is... (page 2)
complex zero is... (page 2)
a complex number is called... (page 2)
a root of degree n of a complex number is called... (p. 10)
the root of the equation is... (p. 14)
the coefficients of the polynomial are... (p. 14)
the imaginary unit is... (page 2)
the imaginary part of a complex number z is... (page 2)
the modulus of a complex number is called... (p. 4)
the zero of a function is called... (p. 14)
the exponential form of a complex number is called... (p. 11)
a polynomial is called... (p. 14)
a simple zero of a polynomial is called... (p. 18)
the opposite number is... (page 2)
the degree of a polynomial is... (p. 14)
the trigonometric form of a complex number is called... (p. 5)
Moivre's formula is... (p. 9)
Euler's formulas are... (page 13)
the entire function is called... (p. 14)
a purely imaginary number is... (p. 2)
Using the calculator
To evaluate an expression, you must enter a string to be evaluated. When entering numbers, the separator between the integer and fractional parts is a dot. You can use parentheses. Operations on complex numbers are multiplication (*), division (/), addition (+), subtraction (-), exponentiation (^) and others. You can use exponential and algebraic forms to write complex numbers. Enter imaginary unit i it is possible without the multiplication sign; in other cases, the multiplication sign is required, for example, between parentheses or between a number and a constant. Constants can also be used: the number π is entered as pi, exponent e, any expressions in the indicator must be surrounded by parentheses.
Example line for calculation: (4.5+i12)*(3.2i-2.5)/e^(i1.25*pi), which corresponds to the expression \[\frac((4(,)5 + i12)(3(,)2i-2(,)5))(e^(i1(,)25\pi))\]
The calculator can use constants, mathematical functions, additional operations and more complex expressions; you can familiarize yourself with these features on the page of general rules for using calculators on this site.
The site is under construction, some pages may not be available.
News
07.07.2016
Added a calculator for solving systems of nonlinear algebraic equations: .
30.06.2016
The site has a responsive design, pages are adequately displayed both on large monitors and on mobile devices.
Sponsor
RGROnline.ru – instant solution to electrical engineering work online.
